LFSR

浅浅学习一下LFSR(线性反馈寄存器)

一分耕耘，一分收获

记录笔者学习LFSR过程

首先了解一下流密码

流密码

流密码它是以最小单位比特作为一次加密、解密的操作元素，利用加密算法进行加密与解密

• 流密码的密钥派生自一个较短的密钥，派生算法通常为一个伪随机数生成算法。
• 流密码的密钥长度会与明文的长度相同。

需要注意的是，流加密目前来说都是对称加密。

伪随机数生成算法生成的序列的随机性越强，明文中的统计特征被覆盖的更好。

流密码加解密非常简单，在已知明文的情况下，可以非常容易地获取密钥流。

流密码的关键在于设计好的伪随机数生成器。一般来说，伪随机数生成器的基本构造模块为反馈移位寄存器(LFSR)。

伪随机数生成器

伪随机数生成器（pseudorandom number generator，PRNG），又称为确定性随机位生成器（deterministic random bit generator，DRBG），是用来生成接近于绝对随机数序列的数字序列的算法。一般来说，PRNG 会依赖于一个初始值，也称为种子，来生成对应的伪随机数序列。只要种子确定了，PRNG 所生成的随机数就是完全确定的，因此其生成的随机数序列并不是真正随机的。

分类

目前主要的伪随机数生成器有：

目前通用的伪随机数生成器主要有

• 线性同余生成器，LCG
• 线性回归发生器
• Mersenne Twister
• xorshift generators
• WELL family of generators
• Linear feedback shift register，LFSR，线性反馈移位寄存器

这里学习一下LFSR

以下学习都是建立在他人博客的基础上

(9条消息) CTF中的LFSR考点(一)_lfsr ctf_沐一 · 林的博客-CSDN博客

LFSR(线性反馈寄存器)

在学习LFSR之前，先了解一下FSR(反馈寄存器)，LFSR是FSR其中一种，另外一种是NFSR(非线性反馈寄存器)

FSR是流密码产生密钥流的一个重要组成部分，在GF(2)上的一个n级FSR通常由n个二元存储器和一个反馈函数组成。

GF(2)指的是有限域2，所以在GF(2)的元素只有0和1

FSR如下图所示：

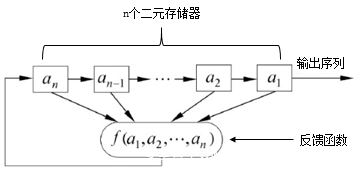
**如果这里的反馈函数是线性的，就称它为LFSR(线性反馈寄存器)**，此时反馈函数可以表示为
$$
f(a_1,a_2,a_3,a_4,a_5) = c_na_1 \oplus c_{n-1}a_2 \oplus…\oplus c_1a_n\\
$$
$$
其中，c_i表示0或1，\oplus表示异或
$$

eg:
$$
假设一个5级的LFSR，其初始状态(即a_1,a_2,a_3,a_4,a_5这五个单元格里面的值)为
$$
$$
(a_1,a_2,a_3,a_4,a_5)=(1,0,0,1,1)
$$

$$
其反馈函数为：
$$

$$
f(a_1,a_2,a_3,a_4,a_5) = a_4 \oplus a_1
$$

整个过程可表示为下面的形式：

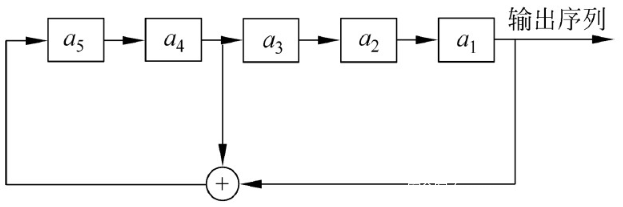
之后，会将反馈函数计算的值作为a6放到a5后面，并且把a1输出，如图：

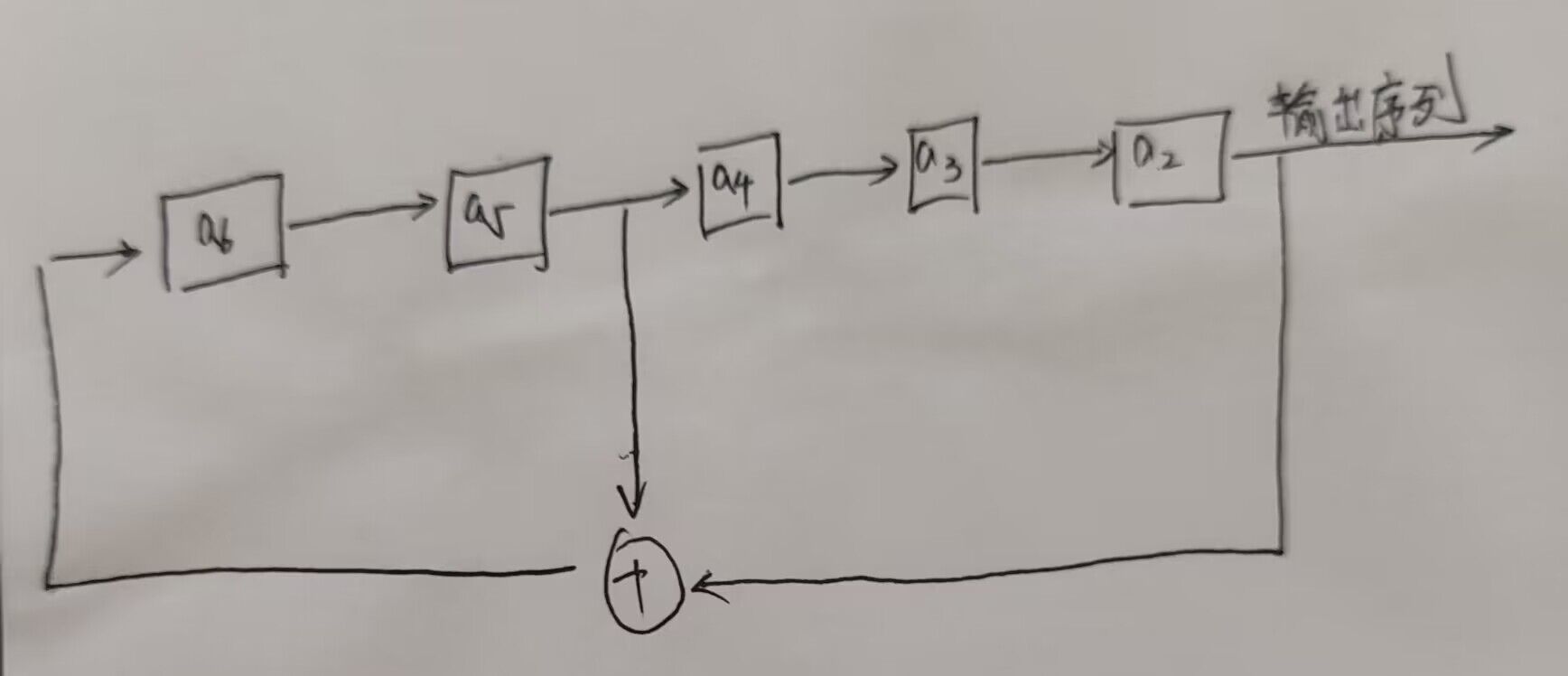
$$
而a_6 = a_4 \oplus a_1 = 1 \oplus 1 = 0
$$

$$
由反馈函数我们可以推出
$$

$$
a_n = a_{n-2} \oplus a_{n-5}(n>5)
$$

$$
通过该函数，我们可以推出剩下的值
$$

$$
经过计算，发现从32位起，之后的数据和前面数据成周期性变化
$$

$$
发现5级LFSR的最大周期为2^5-1
$$

$$
\therefore n级LFSR的最大周期为2^n -1
$$

以下例题是建立在理解别人博客的基础上写的：

原：深入分析CTF中的LFSR类题目（一）-安全客 - 安全资讯平台 (anquanke.com)

例题1 CISCN2018 oldstreamgame

题目

flag = "flag{xxxxxxxxxxxxxxxx}"
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag)==14

def lfsr(R,mask):
    output = (R << 1) & 0xffffffff
    i=(R&mask)&0xffffffff
    lastbit=0
    while i!=0:
        lastbit^=(i&1)
        i=i>>1
    output^=lastbit 
    return (output,lastbit)

R=int(flag[5:-1],16)
mask = 0b10100100000010000000100010010100

f=open("key","w")
for i in range(100):
    tmp=0
    for j in range(8):
        (R,out)=lfsr(R,mask)
        tmp=(tmp << 1)^out
    f.write(chr(tmp))
f.close()

分析已知条件

1. flag包裹的内容为8个16进制数字，就是我们需要求的初始状态的值
2. 反馈函数已知，需要从代码的形式理解为“数学”表达式
3. 已知输出
4. 已知mask

分析代码：

1. output = (R << 1) & 0xffffffff先把R左移，然后和0xffffffff进行与操作，其作用是把R的最高位抹去并在最低位补0，并保留低32位，再把该值赋值给output

假设$R$的值为$\color{red}0\color{black}1101010\quad 11101010\quad 10010001\quad 1011101\color{red}1$

在这串代码作用下首先变成$\color{red}0\color{black}\quad11010101\quad 11010101\quad 00100011\quad 0111011\color{red}0$

2. i=(R&mask)&0xffffffff将R和mask进行与操作，并保留低32位，再把该值赋值给i，这里mask已知

3. lastbit=0
      while i!=0:
          lastbit ^= (i&1)
          i=i>>1

   先看lastbit ^= (i & 1)，和i = i >> 1两串代码作用是把i的每位和1进行与操作，再和lastbit异或

   这里假设$i=1001$，取短一点也能看出规律

   $i和1$进行&操作：$1001$ &$0001$

   得到：$0001$即$1$，再和$lastbit$异或

   还要把$i$右移，变成$0100$

   再和1进行与操作：$0100$ &$0001$

   得到：$0000$即$0$，再和$lastbit$异或

   其实就是从i的最低位向i的最高位依次和1进行与操作(不影响值)，再和lastbit做异或运算，

4. output ^= lastbit将output变量的值和lastbit的值异或，再赋值给output

5. f=open("key","w")
   for i in range(100):
       tmp=0
       for j in range(8):
           (R,out)=lfsr(R,mask)
           tmp=(tmp << 1)^out
       f.write(chr(tmp))
   f.close()
   ​			最后对flag做了100个循环，每次输出一个字符，这样key中有100个16进制数字
   
   
   
   ### 找寻规律
   
   1. **因为mask中只有第3，5，8，12，20，27，30，32位是1，其余都是0**
   2. **mask与R做按位与运算得到i，当且仅当R的第3、5、8、12、20、27、30、32这几位中也出现1时，i中才可能出现1，否则i中将全为0。**
   3. **因为lastbit是i从低位到高位依次和lastbit异或得到的(i中的0可以忽略不计，因为0和任何数做异或运算，得到的结果还是原来的数)，且lastbit的初值为0。当i中有奇数个1的时候lastbit的值为1，当i中有偶数个1的时候lastbit的值为0**
   
   4. **又因为i是由R和mask进行与操作得到的，所以当R中第3，5，8，12，20，27，30，32有奇数个1的时候lastbit为1，有偶数个1的时候lastbit为0**
   
   5. **因此我们可以得出结论，lastbit的值取决于R中第3，5，8，12，20，27，30，32依次异或的结果**
   
   
   
   ### 得到结论
   
   $$
   lastbit = R_3\oplus R_5\oplus R_8\oplus R_{12}\oplus R_{20}\oplus R_{27}\oplus R_{30}\oplus R_{32}
   $$
   
   
   
   这样就得到了反馈函数的"数学"表达式
   0b100000111111011110111011111000101001001100100111110100000010000011111100110011000111011010100000100011100010101110010111101101000010000011110111110000110010110000111001111010100000110011010101010110100101100011010001011101111101000100110101111100000110000110110000011111010001011001101111001110000100110101111100011101101101101100011101100111011101011101010111011100101110101011011110100111100000111110010010001010001000000011110000011001110010100010010111000010001011110110000010101110011000101011001101111101111010001110010000000101011110001110001110100111011110000111111010110100001010010111001100001101100101011100100111100001100101000100001010001000111010110011111000101110011101000111110110000010000101101010010001111000010101010000011110100001001101111011010000010011110011010110100100001100
   **因为这里除去0b只有798位，所以把前面两位换成0即是800位二进制数据，也许是这样理解的吧**
   
   **当即将输出第32位lastbit时，此时R已经左移了31位，所以此时第32位就是原来的第1位**
   
   $last_1 = R_{1,3} \otimes R_{1,5}$
   
   ![](../../images/LFSR/2.png)
   
   **这样我们就可以求出R的第1位，**
   $$
   如果求第一位，应该先是这样:\quad 
   ?0010000011111101111011101111100
   $$
   
   $$
   再变成key=00100000111111011110111011111000
   $$
   
   $$
   根据lastbit = R_3\oplus R_5\oplus R_8\oplus R_{12}\oplus R_{20}\oplus R_{27}\oplus R_{30}\oplus R_{32}
   $$
   
   $$
   \therefore
   R_{32} = R_3\oplus R_5\oplus R_8\oplus R_{12}\oplus R_{20}\oplus R_{27}\oplus R_{30}\oplus lastbit
   $$
   
   $$
   即
   $$
   
   $$
   ? = R_3\oplus R_5\oplus R_8\oplus R_{12}\oplus R_{20}\oplus R_{27}\oplus R_{30}\oplus lastbit
   对这里求解?0010000011111101111011101111100
   $$
   
   $$
   所以R_1 = 1 \oplus 1 \oplus 0 \oplus 0 \oplus 1 \oplus 0 \oplus 0 \oplus 0=1
   $$
   
   
   
   **同样的方法，先右移，我们可以求出R的第2位**
   
   ![](../../images/LFSR/3.png)
   
   **exp:**
   
   ```python
   key = "00100000111111011110111011111000"
   mask = "10100100000010000000100010010100"
   
   R = ""
   tmp = key
   
   for i in range(32):
       newkey = '?'+key[:31]
       m = int(newkey[-3])^int(newkey[-5])^int(newkey[-8])^int(newkey[-12])^int(newkey[-20])^int(newkey[-27])^int(newkey[-30])^int(tmp[-1-i]) #这个tmp[-1-i]是求第i位对应当时lastbit的值
       R += str(m)
       key = str(m) + key[:31]  #这里得到了第1位，求第二位就需要更新key
   
   
   flag = "flag{"+ hex(int(R[::-1],2)) + "}"	#逆序回去
   print(flag)
   
   #flag{0x926201d7}
   #把0x删了
   

总之，理解还没有很清楚

例题2 强网杯2018 StreamGame1

题目

from flag import flag
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag)==25

def lfsr(R,mask):
    output = (R << 1) & 0xffffff
    i=(R&mask)&0xffffff
    lastbit=0
    while i!=0:
        lastbit^=(i&1)
        i=i>>1
    output^=lastbit
    return (output,lastbit)


R=int(flag[5:-1],2)
mask    =   0b1010011000100011100

f=open("key","ab")
for i in range(12):
    tmp=0
    for j in range(8):
        (R,out)=lfsr(R,mask)
        tmp=(tmp << 1)^out
    f.write(chr(tmp))
f.close()

关于这个key的获取，有点疑惑，从bytes_to_long输出之后除了0b是95位，自己手动在最前面添了0

然后根据题目要求的只有19位，所以取前19位

这个lsfr函数和前面CISCN的一样

再根据mask1的位置，写出反馈函数
$$
lastbit = R_3\oplus R_4\oplus R_5\oplus R_9\oplus R_{13}\oplus R_{14}\oplus R_{17}\oplus R_{19}
$$
然后求解就行了

exp:

key = "0101010100111000111"
mask = "1010011000100011100"

R = ""
tmp = key

for i in range(19):
    newkey = '?'+key[:18]
    m = int(newkey[-3])^int(newkey[-4])^int(newkey[-5])^int(newkey[-9])^int(newkey[-13])^int(newkey[-14])^int(newkey[-17])^int(tmp[-1-i])
    R += str(m)
    key = str(m) + key[:18]


flag = "flag{"+ str(int(R[::-1])) + "}"
print(flag)

#flag{1110101100001101011}

还有一种爆破的方法：

用010打开key文件，提取每个值

from Crypto.Util.number import *
from tqdm import *

def lfsr(R,mask):
    output = (R << 1) &0xffffff
    i=(R&mask)&0xffffff
    lastbit=0
    while i!=0:
        lastbit^=(i&1)
        i=i>>1
    output^=lastbit
    return (output,lastbit)
 
key = [0x55,0x38,0xF7,0x42,0xC1,0x0D,0xB2,0xC7,0xED,0xE0,0x24,0x3A]
mask=0b1010011000100011100
 
for k in trange(2**19):
    R=k
    a=''
    judge=1
    for i in range(12):
        tmp = 0
        for j in range(8):
            (k, out) = lfsr(k, mask)
            tmp = (tmp << 1) ^ out
        if(key[i]!=tmp):
           judge=0
           break
    if(judge==1):
        print('flag{'+bin(R)[2:]+'}')
        break

例题3 强网杯2018 StreamGame2

题目

from flag import flag
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag)==27

def lfsr(R,mask):
    output = (R << 1) & 0xffffff
    i=(R&mask)&0xffffff
    lastbit=0
    while i!=0:
        lastbit^=(i&1)
        i=i>>1
    output^=lastbit
    return (output,lastbit)


R=int(flag[5:-1],2)
mask=0x100002

f=open("key","ab")
for i in range(12):
    tmp=0
    for j in range(8):
        (R,out)=lfsr(R,mask)
        tmp=(tmp << 1)^out
    f.write(chr(tmp))
f.close()

和StreamGame1类似，换了flag的长度，并且以16进制的形式给出mask

先求mask,mask = 100000000000000000010

因为mask变了，所以反馈函数变了
$$
lastbit = R_2 \oplus R_{21}
$$
输出key之后，除了0b就是96位，所以直接取前21位

exp1:

key = "101100101110100100001"
mask = "100000000000000000010"

R = ""
tmp = key

for i in range(21):
    newkey = '?'+key[:20]
    m = int(newkey[-2])^int(tmp[-1-i])
    R += str(m)
    key = str(m) + key[:20]


flag = "flag{"+ str(int(R[::-1])) + "}"
print(flag)

#flag{110111100101001101001}

exp2:

from Crypto.Util.number import *
from tqdm import *

def lfsr(R,mask):
    output = (R << 1) &0xffffff
    i=(R&mask)&0xffffff
    lastbit=0
    while i!=0:
        lastbit^=(i&1)
        i=i>>1
    output^=lastbit
    return (output,lastbit)
 
key = [0xB2,0xE9,0x0E,0x13,0xA0,0x6A,0x1B,0xFC,0x40,0xE6,0x7D,0x53]
mask=0b100000000000000000010
 
for k in trange(2**21):
    R=k
    a=''
    judge=1
    for i in range(12):
        tmp = 0
        for j in range(8):
            (k, out) = lfsr(k, mask)
            tmp = (tmp << 1) ^ out
        if(key[i]!=tmp):
           judge=0
           break
    if(judge==1):
        print('flag{'+bin(R)[2:]+'}')
        break

例题4 2018HITB-XCTF

题目

from flag import flag
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag)==47
 
def lfsr(R,mask):
    output = (R << 1) & 0xffffff
    i=(R&mask)&0xffffff
    lastbit=0
    while i!=0:
        lastbit^=(i&1)
        i=i>>1
    output^=lastbit
    return (output,lastbit)
 
 
 
R=int(flag[5:-1],2)
mask    =   0b10110110110011010111001101011010101011011
 
f=open("key","ab")
for i in range(64):
    tmp=0
    for j in range(8):
        (R,out)=lfsr(R,mask)
        tmp=(tmp << 1)^out
    f.write(chr(tmp))
f.close()

lfsr还是没变化，变的是flag的长度和mask

根据mask求出反馈函数
$$
lastbit =R_1\oplus R_2\oplus R_4\oplus R_5\oplus R_7\oplus R_9\oplus R_{11}\oplus R_{13}\oplus R_{14}\oplus R_{16}\oplus R_{18}\oplus R_{19}\oplus R_{22}\oplus R_{23}\oplus R_{24}\oplus R_{26}\oplus R_{28}\oplus R_{29}\oplus R_{32}\oplus R_{33}\oplus R_{35}\oplus R_{36}\oplus R_{38}\oplus R_{39}\oplus R_{41}
$$
呜呜呜有题目没附件

例题5 强网杯2018 StreamGame4

题目

from flag import flag
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag)==27
 
def nlfsr(R,mask):
    output = (R << 1) & 0xffffff
    i=(R&mask)&0xffffff
    lastbit=0
    changesign=True
    while i!=0:
        if changesign:
            lastbit &= (i & 1)
            changesign=False
        else:
            lastbit^=(i&1)
        i=i>>1
    output^=lastbit
    return (output,lastbit)
 
R=int(flag[5:-1],2)
mask=0b110110011011001101110
 
f=open("key","ab")
for i in range(1024*1024):
    tmp=0
    for j in range(8):
        (R,out)=nlfsr(R,mask)
        tmp=(tmp << 1)^out
    f.write(chr(tmp))
f.close()

不同之处在于反馈函数不一样了

我的理解是第一个lastbit一定为0