题目收集
记录一些长知识的题目
easyrandom
1 | from random import Random |
1 | leak = [47945, 50431, 10861, 5794, 26338, 2641, 58647, 52422, 35384, 50426, 58144, 2744, 7864, 25333, 3500, 59273, 38075, 38630, 18760, 19660, 54418, 53538, 20251, 25758, 4500, 14384, 40765, 43841, 62662, 64548, 6468, 8997, 20572, 9920, 64146, 49443, 32054, 56082, 21773, 38390, 14905, 47230, 43126, 37449, 1016, 23685, 48461, 13070, 58381, 51813, 48909, 10953, 31195, 1703, 33439, 54463, 63977, 29188, 44901, 53588, 32843, 9923, 2188, 42503, 53555, 44818, 55094, 40544, 25787, 34965, 65151, 37069, 6342, 36889, 51214, 58386, 34925, 9558, 33552, 29554, 30350, 20166, 4221, 61353, 50656, 7337, 1001, 18279, 27268, 49581, 37870, 54591, 12438, 13649, 42007, 33542, 18118, 48407, 34338, 12147, 19178, 8925, 31109, 12296, 52419, 392, 9296, 16055, 64775, 46394, 58494, 24157, 62237, 16211, 23935, 10368, 48440, 60061, 47813, 49032, 50836, 18404, 30552, 7142, 44142, 44549, 36078, 63112, 28345, 39821, 10004, 32221, 16021, 32152, 53113, 13857, 49328, 11817, 27777, 43088, 43453, 29962, 16338, 44353, 27974, 25145, 56050, 34129, 39236, 46167, 64639, 54581, 33004, 35652, 16294, 11109, 19396, 51476, 30332, 24701, 43628, 44507, 27688, 37172, 61339, 9893, 45217, 7969, 33523, 2495, 15578, 55444, 48564, 5055, 16048, 8512, 1819, 19702, 13388, 41099, 30256, 10592, 46063, 30881, 8338, 41214, 55255, 50060, 65028, 9114, 8417, 43767, 62760, 49830, 50660, 19358, 22142, 53025, 37930, 49155, 2150, 56194, 36251, 49654, 32395, 33677, 48743, 12627, 30575, 64001, 60220, 26908, 44207, 23532, 18430, 45511, 33553, 62631, 55155, 58715, 59152, 20864, 14790, 32774, 48679, 24325, 54109, 2747, 17046, 19083, 60413, 11773, 42188, 17011, 13361, 2105, 23067, 45439, 1122, 54117, 31435, 49692, 59556, 51893, 24342, 11073, 52326, 23237, 22930, 12691, 38125, 36714, 54043, 34880, 53599, 18609, 36631, 24367, 49135, 26821, 64486, 12154, 37534, 14100, 33744, 37183, 7652, 26403, 42166, 12290, 32315, 19153, 55490, 4558, 60768, 44149, 26258, 38676, 31228, 43610, 39357, 36475, 29434, 41437, 64762, 5251, 33641, 43819, 29769, 38136, 8348, 33123, 17571, 18343, 50569, 55502, 7371, 14515, 41553, 12979, 1276, 45454, 56057, 51518, 30382, 30678, 60443, 58274, 50882, 64918, 34569, 58195, 34410, 47490, 13676, 37502, 61987, 7616, 11528, 13577, 51098, 5435, 51972, 63061, 55995, 21627, 2439, 47554, 6891, 53790, 62563, 38921, 30600, 49498, 49671, 38844, 42840, 49982, 16503, 13854, 63825, 25195, 41078, 36872, 36288, 63461, 29293, 28630, 23547, 57332, 43051, 49205, 14579, 23897, 944, 47223, 6819, 61851, 57886, 10858, 14380, 35796, 4509, 52576, 47112, 44349, 56553, 45075, 31505, 2779, 17216, 47395, 15024, 26498, 25299, 26548, 39954, 33242, 65187, 33291, 38861, 6956, 4371, 11762, 41126, 54447, 56384, 34835, 595, 52198, 13324, 38653, 21103, 34301, 20781, 64650, 17773, 1921, 46490, 37683, 27720, 7812, 49737, 20423, 16452, 52475, 27896, 49613, 60121, 54986, 30680, 37740, 8407, 30833, 29431, 62841, 27957, 57755, 59153, 44802, 42423, 28202, 54075, 3879, 25261, 57958, 53266, 22806, 64334, 34962, 57708, 20653, 17925, 59244, 38640, 31264, 7962, 5234, 16995, 35712, 39263, 33764, 9168, 59263, 6297, 28879, 54753, 31041, 42448, 57238, 52395, 61412, 29370, 52297, 21906, 36837, 62511, 13185, 53251, 47459, 47320, 24874, 5152, 63178, 20614, 808, 6789, 37043, 9713, 31692, 18319, 60295, 9628, 1053, 54874, 26808, 28046, 27964, 7534, 43316, 51573, 51143, 41954, 16366, 19618, 23676, 63245, 28329, 25170, 55118, 49376, 22296, 41638, 42595, 49291, 51001, 21173, 17098, 11956, 33292, 28909, 63160, 63480, 32649, 49809, 24112, 59503, 38840, 22914, 17473, 51978, 25420, 64060, 58894, 35793, 57163, 59038, 58787, 64067, 55780, 61906, 1696, 156, 25499, 57706, 47842, 47243, 14668, 17052, 57195, 53288, 49178, 2557, 31221, 17492, 11560, 23012, 9147, 44260, 22094, 53197, 40404, 21209, 30940, 18586, 48011, 60631, 8838, 13044, 5480, 19584, 20231, 15078, 58154, 8305, 55680, 49974, 2861, 58626, 61041, 47937, 42776, 35207, 39418, 12989, 1507, 5082, 23278, 26969, 10328, 18480, 34160, 55965, 59869, 197, 38066, 17097, 49306, 12749, 21846, 9946, 12323, 39813, 19141, 14950, 15987, 33630, 14715, 52499, 15978, 24078, 60217, 32262, 11645, 1649, 50062, 21979, 30545, 1450, 48657, 41697, 23357, 17880, 27613, 38277, 54988, 11074, 57591, 183, 62803, 8532, 61133, 26944, 63400, 53095, 8663, 59702, 19325, 24726, 51297, 21286, 2373, 38774, 20677, 29443, 24693, 20621, 14031, 45485, 34645, 9926, 12620, 1406, 41462, 50338, 25841, 61724, 41722, 11520, 48377, 34111, 50805, 23351, 64363, 50091, 35487, 49978, 41001, 37117, 17133, 54868, 58918, 17295, 16857, 45165, 5732, 46277, 54359, 64982, 2336, 61929, 40501, 18901, 39938, 949, 45839, 7519, 36935, 55287, 21096, 44443, 12240, 16160, 28355, 42275, 27747, 13398, 12395, 33973, 17137, 60697, 37064, 27782, 45671, 22264, 505, 20989, 57585, 4283, 43110, 28497, 25900, 16383, 13961, 24192, 29296, 34776, 36286, 18398, 55882, 28748, 54021, 673, 22723, 23699, 48463, 17316, 55309, 54229, 28342, 11147, 16132, 24344, 53367, 45597, 42843, 27078, 4034, 16975, 18534, 29674, 36962, 60773, 8030, 17118, 7392, 41627, 44768, 51104, 10876, 16293, 54589, 65082, 62573, 2679, 23869, 61905, 52526, 51584, 57063, 27294, 51821, 9070, 30961, 38741, 36309, 57422, 58231, 32775, 57469, 2306, 43632, 6110, 17478, 3399, 60718, 23947, 21488, 41712, 43552, 34154, 35374, 17522, 16603, 53459, 52136, 49823, 21443, 35049, 4854, 25769, 63782, 21355, 11189, 17330, 41173, 6620, 24475, 40910, 26100, 34752, 10491, 39327, 561, 24612, 36253, 41875, 1589, 44536, 64133, 37260, 24719, 21955, 40847, 8529, 12294, 22158, 31784, 32185, 18438, 9983, 9362, 46554, 8294, 11447, 38253, 32008, 44252, 14392, 36259, 40422, 53018, 41387, 61549, 43601, 24082, 64942, 50817, 18470, 52024, 19769, 38618, 54451, 44579, 48552, 52967, 3546, 13047, 19986, 752, 25560, 33608, 55220, 35170, 17378, 3632, 7932, 12764, 28016, 51153, 42067, 22380, 11170, 35549, 14546, 6725, 50718, 40157, 54482, 45086, 50180, 44396, 19469, 48734, 9003, 32234, 4973, 19031, 32744, 15216, 11167, 31666, 50585, 28017, 56213, 23276, 62789, 19240, 52247, 51360, 23933, 2117, 23909, 20136, 11108, 55792, 10848, 42772, 52949, 20973, 49997, 20027, 26803, 34251, 18768, 1273, 21372, 57638, 43004, 27339, 51671, 4505, 7193, 64268, 15856, 9038, 63520, 62076, 41936, 27929, 23469, 55533, 25007, 31555, 15349, 11603, 51345, 44304, 49007, 35765, 50361, 48434, 41407, 41415, 27322, 45767, 56009, 17808, 36797, 55785, 18842, 27904, 55984, 54213, 25742, 30451, 13819, 37675, 23224, 18337, 63137, 40370, 39116, 53931, 7352, 5724, 14040, 13609, 34023, 39058, 59660, 20699, 5752, 594, 53440, 58700, 58977, 11902, 11358, 54271, 52581, 63883, 4496, 65446, 8092, 32955, 1788, 7547, 30827, 42738, 51248, 13433, 52570, 45277, 4811, 59546, 17021, 32981, 6168, 45440, 41446, 43907, 44327, 22960, 48214, 53682, 39618, 65392, 31131, 36083, 31230, 15227, 1530, 21222, 11049, 27763, 5251, 56978, 12249, 55352, 54216, 24824, 65111, 21374, 42945, 57027, 3920, 32541, 65155, 12251, 19929, 19866, 58236, 22788, 54575, 53449, 16521, 55829, 14990, 8653, 55846, 6198, 24332, 28673, 50260, 60726, 55293, 35325, 4142, 28883, 19302, 31711, 10833, 62836, 27199, 14853, 21172, 61281, 43290, 23364, 62192, 58280, 64481, 40708, 17966, 54004, 1651, 1008, 12674, 54156, 48976, 60163, 47799, 14781, 37556, 58786, 14677, 16666, 22398, 41273, 22312, 49859, 4327, 54222, 52527, 35043, 35462, 33939, 30396, 17371, 10883, 42056, 31285, 7486, 33758, 62824, 58144, 19003, 17210, 28590, 39138, 20818, 58339, 7397, 30592, 54635, 33004, 6524, 54578, 21592, 33877, 37330, 51484, 18861, 26317, 426, 6365, 34363, 21922, 33037, 22209, 63283, 6463, 22503, 32397, 54053, 8538, 37449, 39658, 34111, 49684, 27364, 55762, 2892, 64875, 17558, 45202, 37747, 61781, 39006, 5, 55444, 4965, 65360, 45810, 23739, 51172, 37274, 39909, 58863, 28111, 449, 14406, 62190, 13688, 57145, 23653, 56791, 4065, 13079, 59309, 57940, 59317, 17968, 28037, 27233, 53242, 30901, 10758, 57188, 9100, 51760, 16566, 20555, 50514, 35271, 59680, 24646, 14768, 13335, 30246, 39364, 51795, 5031, 38107, 32158, 443, 10384, 6774, 47929, 15499, 50368, 51827, 54022, 18908, 2157, 9827, 14658, 16901, 40891, 5884, 51302, 10387, 10960, 16761, 26793, 55085, 35673, 35137, 13497, 28211, 60579, 60497, 47403, 9106, 59526, 10327, 8063, 41945, 5754, 57621, 26709, 22739, 25547, 24703, 20746, 3895, 44111, 51320, 42212, 59781, 29064, 44610, 16431, 39515, 18156, 14210, 27507, 47206, 41530, 44123, 29499, 47242, 50363, 3339, 57490, 36566, 48636, 49784, 10942, 64447, 26791, 52829, 53204, 55163, 32261, 32157, 58261, 41129, 60614, 30034, 55489, 55576, 25052, 4263, 32514, 1419, 22605, 56589, 48192, 44655, 61295, 8855, 42987, 26448, 33214, 46651, 56194, 28472, 12965] |
exp:
1 | from sage.all import * |
1 | from sage.all import * |
*CTF2022——ezRSA
1 | from Crypto.Util.number import getStrongPrime |
考点是高位攻击,不过没那么明显
高124位
因为q=next_prime(p^((1<<900)-1)^getrandbits(300)),异或并不影响高124位,所以$p$和$q$的高124位一样
思路1
第一种方法是把$n$的前248位进行开根号得到$p,q$的高位
1 | import gmpy2 |
思路2
第二种方法是解方程
先是令$p = p_{h} + p_l$,$q = q_h+q_l$,$p_h = q_h = x$
于是$n = pq = 2^{1800}x^2+2^{900}x×(2^{900}-1+c) + p_lq_l\longrightarrow n = 2^{1800}x^2+2^{1800}x + t$
$t$相对来说比较小,可以忽略,解$n = 2^{1800}x^2 + 2^{1800}x$就可以得到高位
1 | #sage |
中间600位
思路1
对于中间300~900共600位,是不受后面一个异或影响的,p和q每位都是相反的
于是$p+q \approx 2(x<<900) + \color{red}2^{900}-2^{300}$
根据费马分解$n = \frac{(p+q)^2}{4}-\frac{(p-q)^2}{4}$
所以有$\because p-q = \sqrt{4n - (p+q)^2}$,
$\therefore p = \frac{(p+q)+(p-q)}{2} = \frac{2(x<<900)+2^{900}-2^{300}+\sqrt{4n-(p+q)^2}}{2}$
思路2
已知p,q的300~900位是相反的,将这一段设为极端情况——p全为1,q全为0。
根据基本不等式,p、q的差值越大,积就越大
当$pq<n$时,表示这个位置的数正确
1 | import gmpy2 |
低位
最后就是用copper
疑惑点就是这里,两种思路求出这个近似的p之后,不是只差低300位不知道了吗?
为什么small_roots(X)的X上限不是$2^{300}$
最后我觉得的可能应该small_roots()的应用前提是已知576位,然后差了(1024-576 = 448)位,所以把上限定在了
$2^{450}$
三胞胎素数
题目来源[TSGCTF 2021]Beginner’s Crypto 2021
1 | from secret import e |
注意到
1 | assert(isPrime(e)) |
满足这样条件的$e$只有$e=3$
一些定义:
孪生素数
指差等于2的两个素数。
三胞胎素数
指三个连续素数,使得其中最大的一个减去最小一个的差不超过6。
事实上,除了最小的两组三胞胎素数:$(2, 3, 5)$ 和 $(3, 5, 7)$,其它的三胞胎素数都是相差达到6的三元数组。除了以上两个特例以外,三胞胎素数分为两类:
A类三胞胎素数,构成为$p$,$p+2$,$p+6$,相差2的两个孪生素数在前面,例如:$(5,7,11)$;$(11,13,17)$; $(17,19,23)$;等等。
B类三胞胎素数,构成为$p$,$p+4$,$p+6$,相差2的两个孪生素数在后面,例如:(7,11,13);(13,17,19);(37,41,43);等等。
当素数p 大于3时,可以证明形同$p$,$p+2$,$p+4$的数组不可能是三胞胎素数。事实上,这三个数对3的模两两不同,所以必然有一个能被3整除。然而这三个数都比3要大,因此一定有一个是3的倍数,从而这个数不是素数。
详见:三胞胎素数 - 维基教科书,自由的教学读本 (wikibooks.org)
题解
知道$e=3$之后就已知$e_1,e_2,e_3$,然后共模攻击
1 | from Crypto.Util.number import * |
以下是有关论文的题目
N = ma^2 + nb^2 = mc^2 + nd^2
论文:A Note on Euler’s Factoring Problem on JSTOR
另外一个链接:[elementary number theory - A generalization of Euler Factorization with $N = m a^2 + n b^2 = m c^2 + n d^2$ - Mathematics Stack Exchange](https://math.stackexchange.com/questions/4712807/a-generalization-of-euler-factorization-with-n-m-a2-n-b2-m-c2-n-d2#:~:text=John Brillhart discusses a generalization of this method,%3D ma2 %2B nb2 %3D mc2 %2B nd2%2C)
题目来源 NSSCTF#Round11——[ez_fac]
1 | from Crypto.Util.number import * |
论文大体内容就是:
如果$N = ma^2 + nb^2$,且$N=mc^2+nd^2$
$N$即可分解为$N= (N,ad-bc)×\frac{n}{(N,ad-bc)}$,括号就是最大公因数
所以$p = gcd(N,ad-bc)$
本题还需要推导一下e
exp:
1 | from Crypto.Util.number import * |
n = p^r×q
题目来源[D^3CTF 2022] ——d3factor
1 | from Crypto.Util.number import bytes_to_long, getPrime |
论文内容及证明过程

论文大致内容就是对于$N = p^rq$,当两个解密密钥$d_1$,$d_2$差值不超过$N^{\frac{r(r-1)}{(r+1)^2}}$
即$|d_1-d_2| < N^{\frac{r(r-1)}{(r+1)^2}}$的时候,可以在多项式的时间内分解出$p$
其证明过程如下:
$\because N =p^rq$,$\phi(N) = p^{r-1}(p-1)(q-1)$
有
$$
\left{\begin{matrix}
e_1d_1 \equiv 1 \mod \phi(N) \quad ①\
e_2d_2 \equiv 1 \mod \phi(N) \quad ②\
\end{matrix}\right.\
$$
把①式乘$e_2$,②式乘$e_1$再相减得
$e_1e_2(d_1-d_2)-(e_2-e_1) \equiv 0 \mod \phi(N)$
根据论文,把$\phi(N)$用$p^{r-1}$替代掉
则有$e_1e_2(d_1-d_2)-(e_2-e_1) \equiv 0 \mod p^{r-1}$
$d_1-d_2$就是$e_1e_2x - (e_2-e_1) \equiv 0 \mod p^{r-1}$的根
可以用coppersmith求出$x$
然后计算$gcd(e_1e_2x - (e_2-e_1),N) = gcd(k×p^{r-1}(p-1)(q-1),p^rq) = g$
利用这个g
$$
p =
\left{\begin{matrix}
g^{\frac{1}{r-1}},\quad if\quad g = p^{r-1}\
g^{\frac{1}{r}},\quad if \quad g = p^r\
\frac{N}{g},\quad if\quad g = p^{r-1}q
\end{matrix}\right.
$$
本题解答
根据
1 | N = pow(p, 7) * q |
可以判断出$|d_1-d_2|\approx 1000bit$,$N= 2048bbit$,所以$|d_1-d_2|<N^{\frac{r(r-1)}{(r+1)^2}} \approx 1344bit $
满足论文条件
1 | from Crypto.Util.number import * |
$\because g = 1534bit$,$\therefore p = g^{\frac{1}{6}}$
RSA与格结合,且多组n,e,c
题目来源[NUSTCTF 2022 新生赛]——lattice
题目
1 | from Crypto.Util.number import * |
令$M = \sqrt{N_{max}}$,$M$是一组$N$中最大的$N$并且开根号。这组$N$满足:$N_1<N_2<\dots<N_r <2N_1$
又$\because e_id \equiv 1 (\mod \phi(N_i))$
这里把它写成$e_id = 1+k_i\phi{N_i}$
假设$\phi(N_i)$可以写成$k_i(N_i-s_i)$的形式。其中$|s_i<3N_i^{\frac{1}{2}}|$
则$e_id = 1 + k_i(N_i-s_i)$
化简得$e_id-k_iN_i = 1-k_is_i$
所以我们有$r+1$个等式:
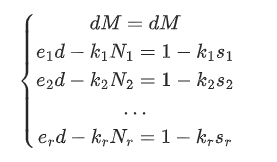
写成矩阵相乘的形式
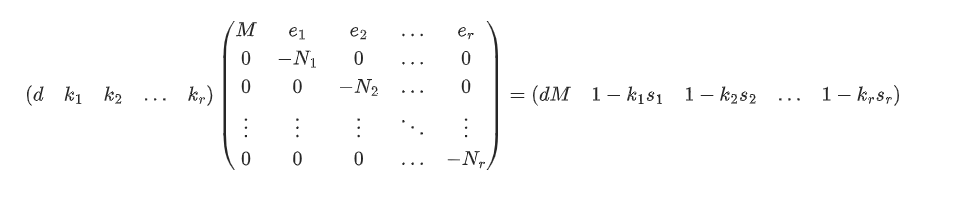
因为最后的目标向量满足LLL算法,所以我们可以得到$dM$
求得$dM$之后,我们可以求得$d$
exp:
1 | import libnum |
cve of RSA
论文:The Return of Coppersmith’s Attack:Practical Factorization of Widely Used RSA Moduli (muni.cz)
如果p,q是以$p = k×M + 65537^a \mod M$的形式产生的,M是个光滑数
攻击脚本:jvdsn/crypto-attacks: Python implementations of cryptographic attacks and utilities. (github.com)
根据结论调参

1 | from secret import flag |
exp:
1 | import logging |
这个脚本我是在sagemath跑的
得到p,q后有手就行
1 | from Crypto.Util.number import * |
有限域上的不可约多项式RSA体制
TCTF2019——babyrsa
1 | #!/usr/bin/env sage |
1 | from sage.all import GF, PolynomialRing |
R.fetch_int(m_int):把整型数据转化成环R上的元素
R(c_poly).integer_representation():把环R上的元素变成整型数据
exp:
1 | from Crypto.Util.number import * |
watevrCTF 2019——Swedish RSA
1 | flag = bytearray(raw_input()) |
out = R.random_element(degree=deg),作用是从一个给定的环或域 R 中生成一个随机元素,并限定该随机元素的次数(degree)。就是会生成一个环R中次数不超过deg的多项式
is_irreducible():作用是判断一个多项式是不是不可约的,如果是不可约的就返回True
R.quotient ,用于计算环或域 R 的商环或商域
先把N分解了,得到一个65次的多项式和一个112次的多项式。
然后重点是计算$\phi(N)=\phi(p)×\phi(q)$
1 | 对于整数n来讲,欧拉函数phi(n)表示所有小于或等于n的正整数中与n互质的数的数目。 |
这篇论文指出了欧拉函数的计算方法
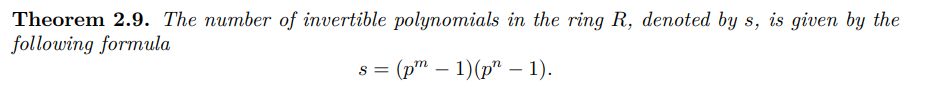
本题中,$p$,$q$都是环R上的多项式,而且$p$,$q$都不可约
$\therefore \phi(N) = (p^{65}-1)×(p^{112}-1)$
然后就是常规RSA解法(我表示很震惊),而且最后 flag的提取也很奇怪
exp:
1 | #sage |
m.list()是把m这个多项式中每一项的系数按照次幂上升的顺序进行排列
2021强网拟态——OnlyRSA
1 | #!/usr/bin/env python |
exp:
1 | n = |
coppersmith
恢复OAEP私钥
题目来源:[蓝帽杯 2022 初赛]corrupted_key
1 | from Crypto.PublicKey import RSA |
priv.pem:
1 | -----BEGIN RSA PRIVATE KEY----- |
私钥文件缺失信息
上网找pem文件的解析
PKCS#1的私钥文件包含以下信息:
1 | RSAPrivateKey ::= SEQUENCE { |
标签头:
1 | 3082025C# 标签头 |
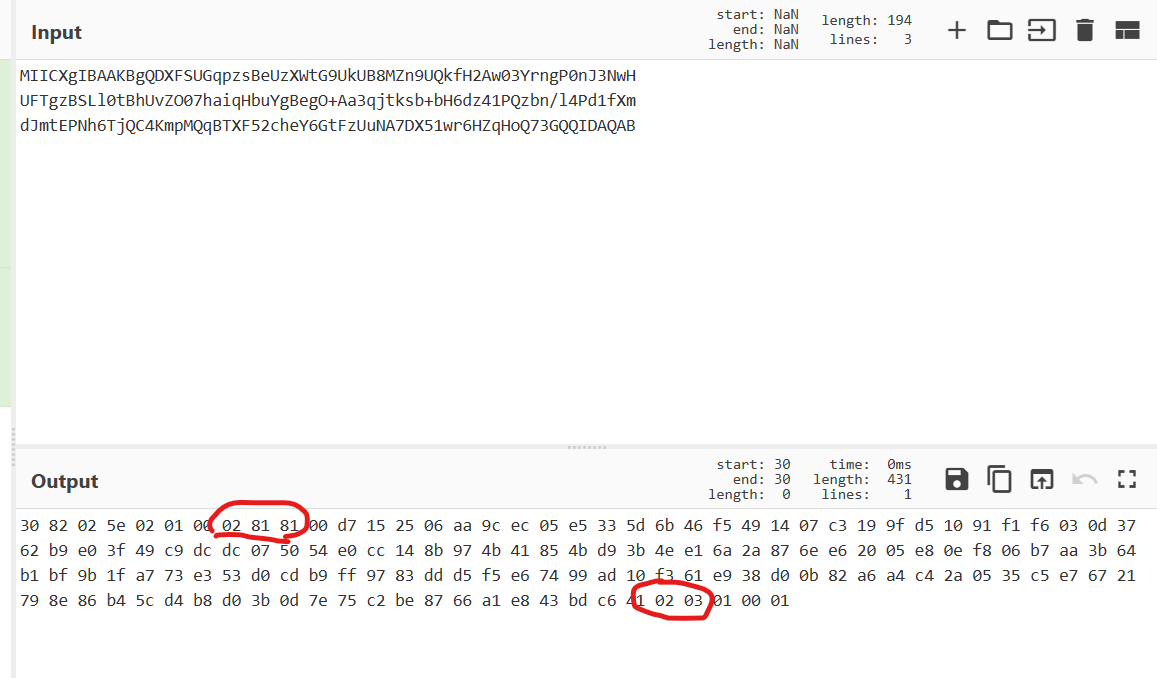
把priv的内容base64解码,再转16进制,并且根据标签头提取信息:
1 | n = 0xd7152506aa9cec05e5335d6b46f5491407c3199fd51091f1f6030d3762b9e03f49c9dcdc075054e0cc148b974b41854bd93b4ee16a2a876ee62005e80ef806b7aa3b64b1bf9b1fa773e353d0cdb9ff9783ddd5f5e67499ad10f361e938d00b82a6a4c42a0535c5e76721798e86b45cd4b8d03b0d7e75c2be8766a1e843bdc641 |
即已知$dq \equiv d \mod (q-1)$,$q^{-1} \mod p$,需要注意的是这里的dq不是完整的dq,而是低120位
$\because dq \equiv d \mod (q-1)$,$dq = d+k(q-1)$
$\therefore dq × e = ed + kd(q-1)$即$dq ×e = k_1(p-1)(q-1) + 1 + kd(q-1)$,可以写成$dq ×e = k(q-1) + 1$
$\therefore dq ×e + k-1 = kq$
两边同模$2^{120}$得$dq×e+k-1 \equiv kq \mod 2^{120}$
$\therefore q \equiv k^{-1}(dq×e +k-1) \mod 2^{120}$
$\because dq < q-1 ,\therefore e > k$
于是我们便能求出$q$的低120位的可能取值
$\because inv ×q \equiv 1 \mod p $,即$inv×q -1 = kp$,两边同乘q得$inv×q×q -q = kn$
即$inv × q×q -q \equiv 0 \mod (n)$
于是可以用coppersmith恢复求得q
区别于$inv×q-1 \equiv 0 \mod p$
exp:
1 | #sage |
参考:(PKCS1) RSA 公私钥 pem 文件解析 - 知乎 (zhihu.com)
comedy(先搁着)
题目
1 | import gmpy2, libnum |
高位攻击
1 | from secrets import flag |
p高位泄露,未知位是128bit
exp:
1 |
|
在异或基础上夹杂移位
1 | from secret import flag |
看到异或就想起LitCTF那道Babyxor,但这题不大一样,因为把m进行了左移操作
因为m左移444位,这样子m后面444位都是0,所以异或之后,不影响p低位444值
而且54长度的flag转成int型数据是432,左移444位后是876位,异或之后p高(1024-876)=148位也是不变的
所以考点就是p部分高位和部分低位泄露
先取了444低位:plow = p0 % 2^445
然后得到148高位:phigh = (p0 >> 876) << 876
exp:
1 | import gmpy2 |
高位攻击结合加法
1 | from Crypto.Util.number import * |
先从p,r入手,因为p(1024bit)的比特远大于r(256bit)的比特,即p的前768位(并不一定是这么多)并不受到r的影响,可用coppersmith恢复p
得到p后,看定义的函数,就是一个不知道多少次的lcg加密过程
n = n << (nbits - n.bit_length())这里保证了模数n足够大,因为再加密过程中,如果n不够大的话,会导致明文的数据丢失一些
再用q解密,需要注意的是用q解密的时候,这个n已经是移位过后的n
exp:
1 | import gmpy2 |
二元copper
参考:二元coppersmith - 顶真珍珠 - 博客园 (cnblogs.com)
代码:
1 | def small_roots(f, bounds, m=1, d=None): |
其中m为移位(shifts),d 为多项式中的最高幂。
[CISCN 2021华南]small
1 | import random, hashlib |
题目给出$x,y$都介于$2^{70}$和$2^{71}$之间
exp:
1 | import hashlib |
P,Q产生方式由拼接而成
这里只是做个记录
原文:CTFtime.org / Crypto CTF 2021 / Hamul / Writeup
Hamul
1 | #!/usr/bin/env python3 |
注意到,PP,QQ的产生方式:
令$x=str(P),y=str(Q)$,于是能把P,Q写成这样的形式:$P=10^xp + q$,$Q=10^yq+p$
再令$x’ = str(PP),y’=str(QQ)$,于是$PP = 10^{x’}P+Q$,$Q=10^{y’}Q+P$
$\because N = PP×QQ$,这个N可以写成$10^{x+x’+y+y’}pq+…+pq$,每一项都含有pq。
因为$x+x’+y+y’$很大,所以存在$str(N)[:?]=str(pq)[:?]$,$str(N)[?:]=str(pq)[?:]$
测试发现$str(N)[:18]=str(pq)[:18]$,$str(N)[-18:]=str(pq)[-18:]$
也有出现前18位,后19位一样,前19位,后18位一样的情况
因为$len(str(pq))=38或39$,可以爆破两位的方式求得pq
exp:
1 | from Crypto.Util.number import * |
HamburgerRSA
1 | from Crypto.Util.number import * |
类似上面那道题
不同的是爆破位数变成了1
1 | from Crypto.Util.number import * |
根据题目改点东西
黑盾杯2020 Change
1 | from flag import FLAG |
记$p$的高位为$ph$,低位为$pl$,易知$ph$,$pl$都是$10^{200}$左右的数
则$p = ph×10^{200}+pl$,$q = pl×10^{200}+ph$
于是$n = (ph×pl)×10^{400}+ph^2×10^{200}+pl^2×10^{200}+ph×pl$
因为$n$大概是$10^{800}$大小的数
记$ph×pl$的高位为$pph$,低位为$ppl$,都是$10^{200}$左右的数
$pph = \frac{n}{10^{600}}$,$ppl = n % 10^{200}$
求出$pph$和$ppl$后,即可求得$ph×pl$
再联立$n = (ph×pl)×10^{400}+ph^2×10^{200}+pl^2×10^{200}+ph×pl$
求解$pl和ph$
exp:
1 | from sympy import symbols,solve |