密钥交换协议(DH)

简述密钥交换协议(DH)

参考文章：

[(8条消息) Diffie-Hellman密钥交换协议及其中间人攻击_Memories off的博客-CSDN博客](https://blog.csdn.net/happy_single/article/details/106175275?ops_request_misc=&request_id=&biz_id=102&utm_term=密钥交换协议 中间人攻击&utm_medium=distribute.pc_search_result.none-task-blog-2allsobaiduweb~default-0-106175275.142^v9^control,157^v4^new_style&spm=1018.2226.3001.4187)

离散对数 ｜ DH ｜ ElGamal | Harry’s Blog (harry0597.com)

密钥交换协议不是一种加密明文的算法，而是生成一个较为安全的密钥的算法

流程

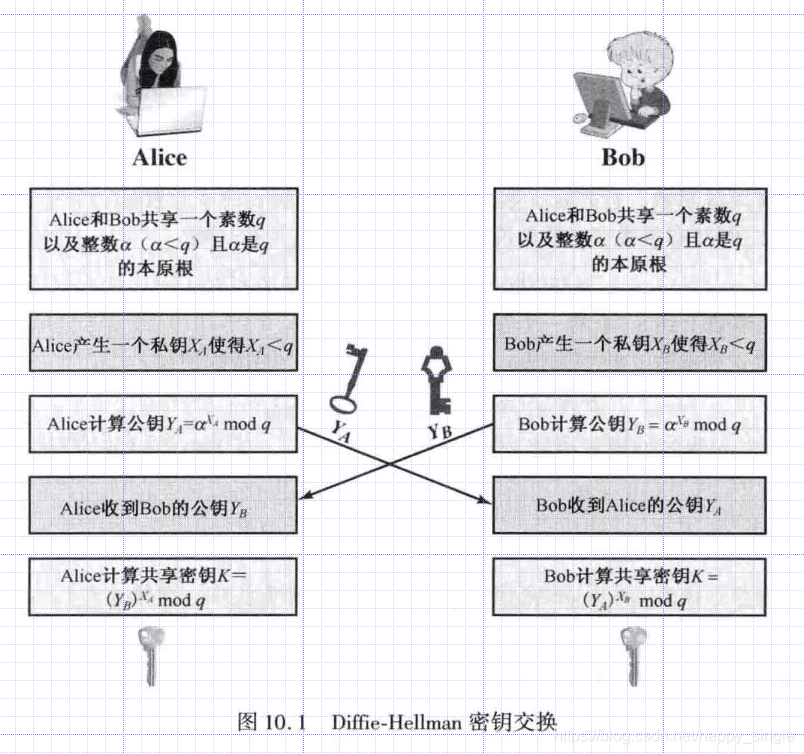
Diffie-Hellman的安全性是基于离散对数求解的困难性的，然而，存在可能的中间人攻击，对Diffie-Hellman协议的安全性造成威胁。

中间人攻击

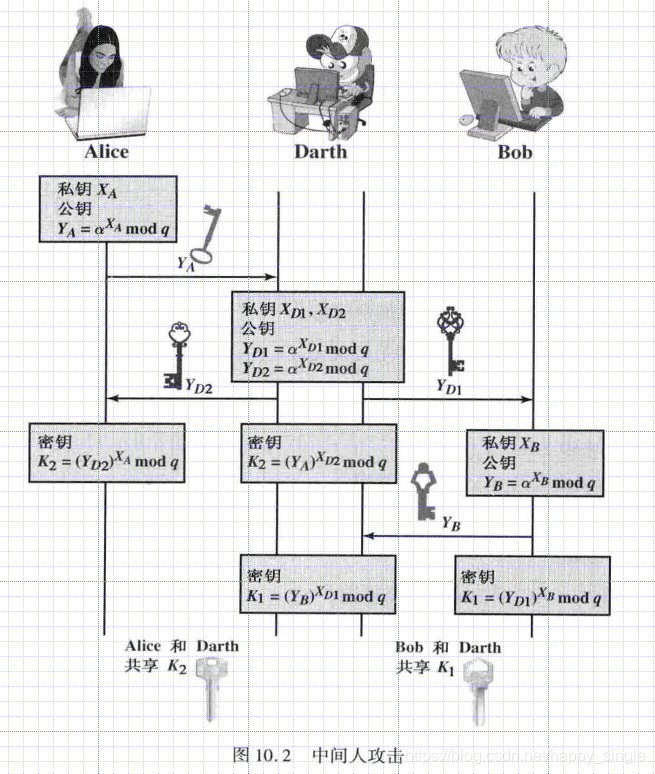
简述一下攻击流程

$$
假设攻击人为Darth
$$

$$
1.Darth截取了Alice发给Bob的公钥Y_A
$$

$$
2.Darth选取了自己的私钥X_{D_1},并计算Y_{D_{1}}=g^{X_{D_1}} \mod p
$$

$$
3.Darth把Y_{D_{1}}发送给Bob，同时Darth计算\color{red}K_2=Y_A^{X_{D_2}} = g^{X_AX_{D_2}}\mod p
$$

$$
4.Bob收到Darth发送的Y_{D_1},并计算\color{blue}K_1 = Y_{D_1}^{X_B} = g^{X_{D_1}X_B} \mod p
$$

$$
5.Bob把Y_B发送给Alice
$$

$$
6.Darth截取Y_B,并把Y_{D_2}发送欸Alice。Darth计算\color{blue}K_1 = Y_{B}^{X_{D_1}} = g^{X_B{X_{D_1}}} \mod p
$$

$$
7.Alice收到Y_{D_2},并计算\color{red}K_2=Y_{D_2}^{X_A} = g^{X_{D_2}X_A}\mod p
$$

$$
此时,Alice和Bob移位他们共享了密钥，但实际上却是:
$$

$$
\color{red} Alice和Darth共享密钥K_2
$$

$$
\color{blue} Bob和Darth共享密钥K_1
$$

$$
接下来，Alice和Bob之间的通信将以下列方式泄密：
$$

$$
1.Alice发送了一份加密的消息M:E(K_2,M),表示用密钥K_2对消息M加密
$$

$$
2.Darth截获了该密文，并解密，知晓了M
$$

$$
3.Darth把E(K_1,M)或者把E(K_1,M’)发送给Bob，其中M’是修改后的信息
$$

$$
如果Darth把E(K_1,M)发送给Bob，表明他只是偷听消息，而没有进行修改
$$

$$
如果Darth把E(K_1,M’)发送给Bob，说明他修改了Alice原本想传给Bob的消息
$$