初识格
记录笔者学习Lattice的过程,好记忆不如烂笔头
格的定义
给定$n$维空间中$n$个线性无关向量:$\vec{b_1},\vec{b_2},…,\vec{b_n}$,并把这$n$个向量称为基
对于这一组向量,存在线性组合$x_1\vec{b_1}+x_2\vec{b_2}+\dots+x_n\vec{b_n}$
我们把整系数的线性组合构成的集合称为格即$x_i \in \mathbb{Z}$
$$
记为\mathcal{L}(B) =
\begin{Bmatrix}
x_1\vec{b_1}+x_2\vec{b_2} + …+x_n\vec{b_n} ,x_i \in \mathbb{Z}
\end{Bmatrix}
$$
举个例子
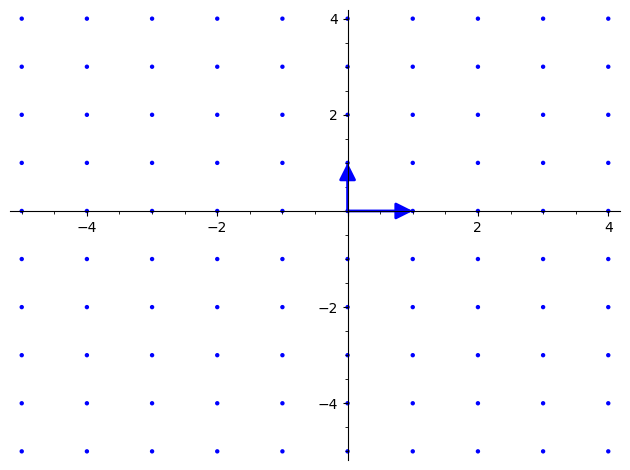
上图为2维空间中的一个格,这个格的基为$(0,1)和(1,0)$
需要注意的是,不同的基有可能生成同样的格。
同样是这个二维空间的格,我们可以用下面这个基构成
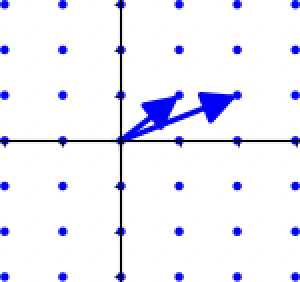
这组基为$(1,1)$和$(2,1)$
这里提出一个问题,什么样的基可以生成同样的格?即格基的等价变换问题
格基的等价变换
- $\color{red}列向量交换$,即$\vec{b_i}\longleftrightarrow \vec{b_j}$
这里给出二维空间中的例子
上述格基$\vec{b_1} =(0,1),\vec{b_2}=(1,0)$,现在令二者交换,即$\vec{b_1} =(1,0),\vec{b_2}=(0,1)$
显而易见,两组格基产生的格是一样的
- $\color{red}向量取反$,即$\vec{b_i} \longleftrightarrow {-\vec{b_i}}$
还是上述例子,$\vec{b_1} = (0,1)$,现在令$\vec{b_1}’ = -\vec{b_1} = (0,-1)$
显而易见,变换之后的基产生的格是一样的
- $\color{red}整系数线性组合$,即$\vec{b_i} \longleftrightarrow \vec{b_i} + k \vec{b_j}$
对于上述基$\vec{b_1}=(0,1),\vec{b_2}=(1,0)$构成的格中
取格点$(4,3)$
现将$\vec{b_1} \longleftrightarrow \vec{b_1}+2\vec{b_2}$,即新的格基为$\vec{b_1}’=(2,1),\vec{b_2}’=(1,0)$
则格点$(3,4)$对于新的格基有了新的线性组合$(3,4)=3\vec{b_1}’-2\vec{b_2}’$
但还是在这个新基的产生的格点上
上述3个方法可以概括为格基矩阵B右乘一个幺模矩阵U(行列式为$±1$的矩阵)
对于上述例子有下式
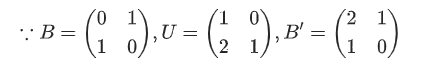
且$||U||=1$
$\therefore$格基$B$和格基$B’$等价
由此我们可以得到结论
两个格基产生相同格的条件
如果格基矩阵$B_1,B_2$满足$B_2=B_1U$,则两格基产生的格一样
格的基本区域
给定格基B产生的格,我们可以确定基础平行多面体,设为P(B),$P(B) =
\begin{Bmatrix}
a_1\vec{b_1}+a_2\vec{b_2} + … +a_n\vec{b_n}\quad |(0 \le a_i <1)
\end{Bmatrix}$
可以理解为最小重复单元
下面给出二维空间中某个格的基本区域
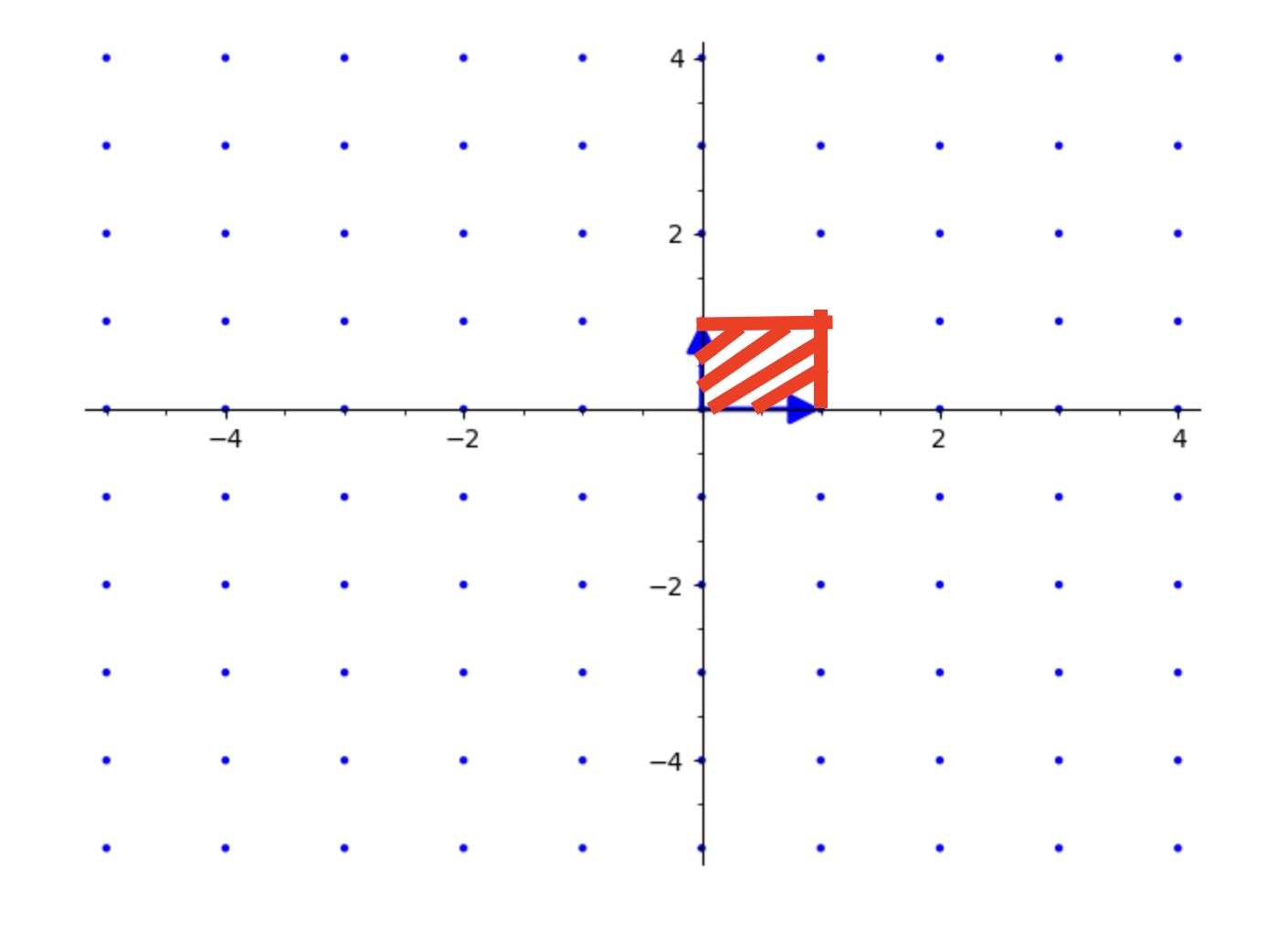
上图中,红色区域就是这个格的基本区域
当我们把基本区域放到的每个格点中,则会遍布这个二维空间
基本区域有什么用呢?
我们发现,当在格中随便取一点$k$,我们都可以把他映射到基本区域中的某个点中
例如$k(3.5,2.4)$,其映射在基本区域的点就是$k’(0.5,0.4)$

映射后:
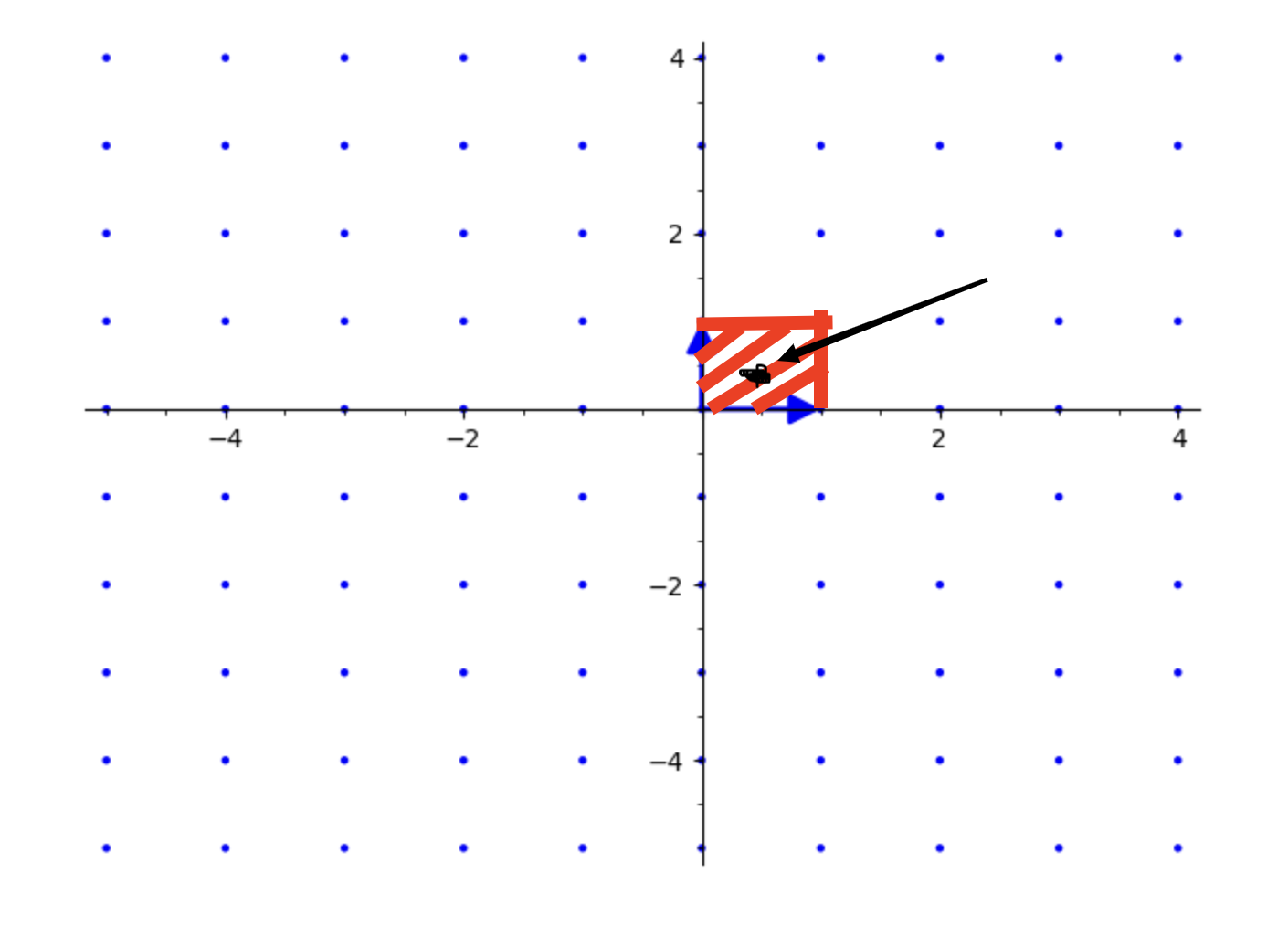
上面的操作可归纳为:
$$
k = m_1\vec{b_1}+m_2\vec{b_2}+…+m_n\vec{b_n}
$$
映射:
$$
k’ = (m_1 \mod 1)\vec{b_1}+(m_2 \mod 1)\vec{b_2} +…+(m_n \mod 1)\vec{b_n}
$$
除此之外,我们可以发现,在一个基本区域中,不存在两个等价的点
行列式
格的行列式指的是基本区域的体积
由上面格基产生相同格的条件,我们可以推断出他们的行列式相同
$\because B_2 = B_1U$
$\therefore det(B_2)=det(B_1)det(U)=det(B_1)$
行列式越小,格点的密度越大
延展空间
我们称格$\mathcal{L}(B)$中基向量的所有线性组合所形成的集合为这组基向量所张成的延展空间(span)
即$span(\mathcal{L}(B)) =
span(B)=
\begin{Bmatrix}
a_1\vec{b_1}+a_2\vec{b_2}+…+a_n\vec{b_n}|a_i\in \mathbb{R}
\end{Bmatrix}$
Successive Minima(连续极小)
由于格上的点是离散的,所以除了零向量外肯定存在一个非零向量,其长度是最短的。
我们定义$\lambda_1(\mathcal{L})$为格$\mathcal{L}$中最短非零向量的长度**(这里不考虑零向量)**
这里的长度指的是欧几里得范数
准确的说,应该是最短非零向量集,因为有一个最短非零向量就有两个(这个向量取反)
因此,在$n$维格中,我们有$2n$个最短向量,每个轴上都有两个最短向量
给个二维空间中的例子来理解
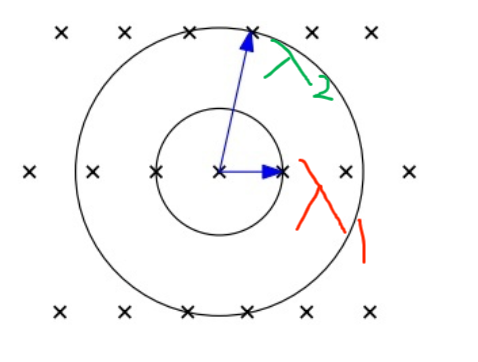
定义
在格$\mathcal{L}$中,第$i$连续极小值$(i=1,2,\dots,n)$,为$\lambda_i=min{r:dim \enspace span(\mathcal{B}(r))\cap \mathcal{L}\ge i}$
定义是比较抽象的
在定义中,$\mathcal{B}(r)$表示半径为$r$的超球体,该超球体和格$\mathcal{\mathcal{L}}$交集产生的向量张成(span)的空间的维度(dim)为i
换言之,第i个连续极小值即包含至少i个线性无关格向量的最小球半径
以下图为例
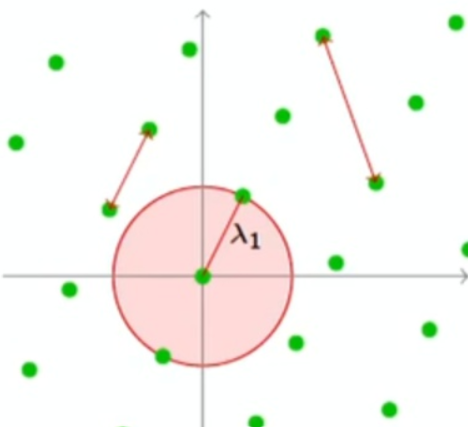
把球的中心放在原点,若球中有非零格向量,那么球中不止一个格向量。以上图为例,红色区域包含了一个非零格向量以及它的逆向量,但这二者在同一条直线上,仅张成一维空间,该超球体的半径是$\lambda_1$
而下图中,一个更大的超球体包含了4个非零格向量,可以张成二维空间,该超球体的半径是$\lambda_2$
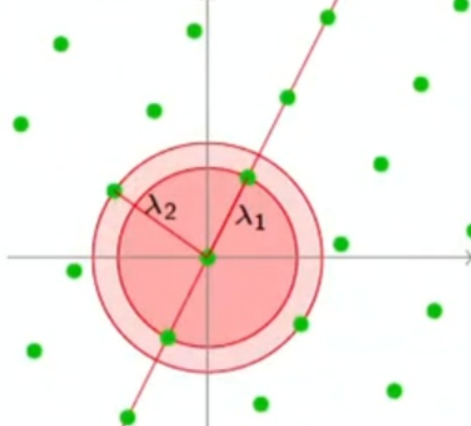
对这个概念模糊不清
重点是要知道$\lambda_1(\mathcal{L})$指的是格$\mathcal{L}$最短非零向量的长度
施密特正交化给出格中最短非零向量长度的有效下界
施密特正交化
其作用是把一组基转换成一组正交基。学了线性代数这门课的话理解起来并不难。
这里给出二维空间中的一个例子:
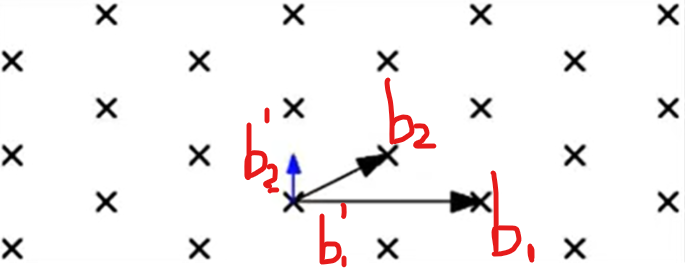
如图,把原来一组基$\vec{b_1},\vec{b_2}$,转换成$\widetilde{b}_1,\widetilde{b}_2$这一组正交基
过程如下
首先,给定一组线性无关的向量$\vec{b_1},\vec{b_2},…,\vec{b_n}$
然后通过计算得到一组正交基$\widetilde{b}_1,\widetilde{b}_2,…,\widetilde{b}_n$
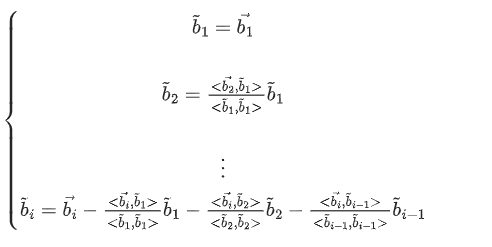
$<\vec{b_i},\vec{b_j}>$表示$\vec{b_i}$与$\vec{b_j}$的内积
我们令$\mu_{i,j}=\frac{<\vec{b_i},\widetilde{b}_j>}{<\widetilde{b}_j,\widetilde{b}_j>}$
则正交化向量可表示为
书上的解释(虽然有些杂乱,也可参考参考):

值得一提的是,施密特正交化能将基正交化,但并不能直接应用于格基,因为正交化过程中系数并没限制为整数,也就是 格基 施密特正交化后的结果很可能不在格上
下面讲施密特正交化的应用
QR分解
对于格而言,先对格基$\vec{b_1},\vec{b_2},…,\vec{b_n}$间接使用施密特正交化 ($\color{red}施密特正交化过程中,没有保证系数都是整数,我们需要对其取整$)
之后我们能得到近似正交基$\widetilde{b}_1,\widetilde{b}_2,…,\widetilde{b}_n$
把他写成矩阵形式为

本质上,QR分解形式的矩阵是格基的另一种矩阵表示法,上图中每个列向量都是格基
结论如下
- 该矩阵是上三角行列式所以行列式$det(B) = \prod_{i=1}^{n}||\widetilde{b}_i||$
- 我们能得到$\lambda_1$的下界,即$\lambda_1\ge min(||\widetilde{b}_i||)$
我的理解是,既然得到了近似正交基,那我把$min(||\widetilde{b}_i||)$这个基之外的基全部取0,是不是就能得到$\lambda_1$了
更严谨的证明:

看不懂证明就这样吧,总之我们得到了$\lambda_1$的下界
格中难题
SVP最短向量问题(Shortest Vector Problem)
SVP,最短向量问题,准确的说是最短非零向量问题。定义如下
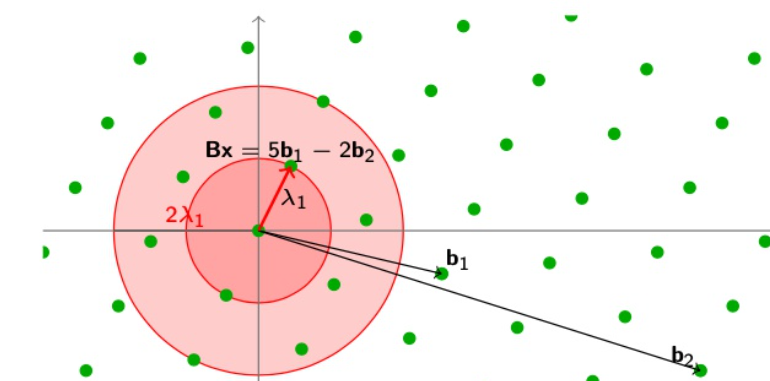
给定一个基为$B$的格$\mathcal{L}(B)$,找到一个这个基构成的格点,使得这个点离0坐标点的距离最近,即$||Bx||\le \lambda_1$
因为$\lambda_1$是格点之间的最短距离,所以Bx距离0点的距离并不会小于$\lambda_1$,最多等于$\lambda_1$
最短向量是存在上界的
Hermite定理
这个定理给出了最短向量的上界,定理内容如下
对于n维的格$\mathcal{L}$,都包含一个非零向量$\vec{v} \in \mathcal{L}$,满足$||\vec{v}|| \le \sqrt{n}det(\mathcal{L})^{\frac{1}{n}}$

上图中,格的基向量$B=[b_1,b_2]$,我们找到了$Bx=5b_1-2b_2$这个点,正好就是格的最短向量λ1
对于某些不太好的格来说,严格计算SVP是件很苦难的事,于是有了要求宽松一点的$SVP\gamma$问题
定义如下:
给定一个基为B的格$\mathcal{L}(B)$,找到一个这个基构成的格点,使得这个点离0坐标点的距离$\le \gamma\lambda_1$
$||Bx|| \le \gamma \lambda_1$
$$
如图所示,当\gamma=2时,SVP_\gamma问题有了很多解
$$
高斯启发式
高斯启发式是对赫米特定理的进一步缩小
假设L是n维格,高斯所期望的最短的长度是
$\sigma(L) = \sqrt{\frac{n}{2\pi e}}(Det(L))^{\frac{1}{n}}$
高斯启发式表示,在一个“随机选择的格”中的最短非零向量满足
$||\vec v_{shortest}|| \approx \sigma(L)$
CVP最近向量问题(Closest Vector Problem)
定义如下:
给定连续空间中任意的一个点t,找到距离这个点最近的格点Bx,满足$||Bx-t|| \le \mu$
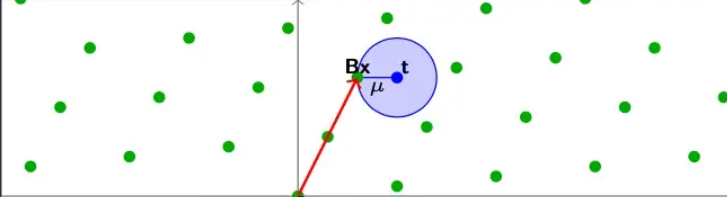
这里我们的约束距离$\mu$就是这个Lattice的覆盖半径(即所有可能的t中距离格点最长的距离)。
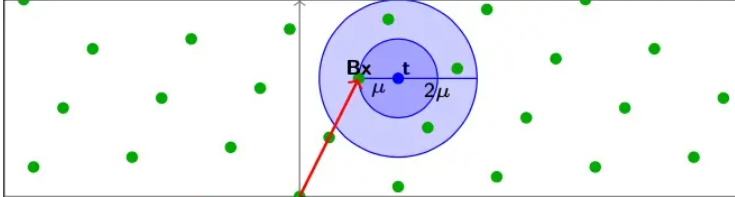
同理我们有要求宽松点的$CVP\gamma$问题
定义如下:
$$
||Bx-t|| \le \gamma\mu
$$
$$
这个图很好表示了当\gamma=2的情况下,我们找到了更多满足CVP的点
$$
加上一个宽松的参数$\gamma$之后,CVP问题就会变得简单一些,解的数量也变多了。
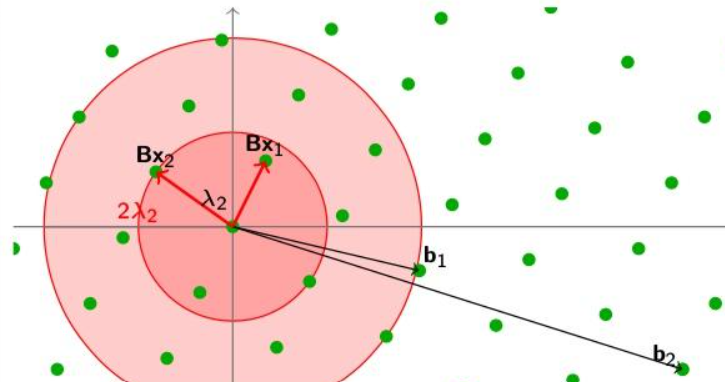
SIVP最短独立向量问题(Shortest Independent Vector Problem)
定义如下
$$
给定一个格\mathcal{L}(B),找到n个线性独立的向量Bx_1,Bx_2,…Bx_n并且这些向量的长度都要小于等于最长的最短向量
$$
$$
max||Bx_i|| \le \lambda_n
$$

$$
这个图很好表达了当n=2的情况下,我们找到了两个小于等于\lambda_2的点
$$
$$
同理,我们有SIVP_\gamma问题
$$
$$
在SIVP_\gamma问题中,我们只需要找到\gamma \lambda_n范围中的格点即可
$$
LLL算法
首先,我们知道一个格可能有很多基,这些基里面,肯定有好坏之分

比如上图中,蓝色的基明显就比绿色的基好。
这是因为
- 蓝色的基向量更短
- 蓝色的基夹角更大,即正交性更好,这会帮助我们更好地观察格
LLL算法的目的
在n维空间中,LLL算法要做的是让施密特正交化的程度最大化
官方解答是,LLL算法要找一个基,使得Gram-Schmidt向量的正交程度不会下降太快
以下是LLL规约基的样子

这其实就是施密特正交化的过程
B这个基可以写成一个正交向量构成的矩阵,乘上一个幺模矩阵
LLL规约基拥有的性质
所有$|\mu_{i,j}|\le \frac{1}{2}$
向量长度满足这样关系:
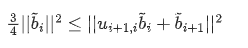
性质2大概的意思就是得到的向量不能太短
两个性质综合起来的结论是$||\widetilde{b}_{i+1}||^2 \ge \frac{1}{2}||\widetilde{b}_i||^2$
这就是LLL算法?????????????对此我十分疑惑
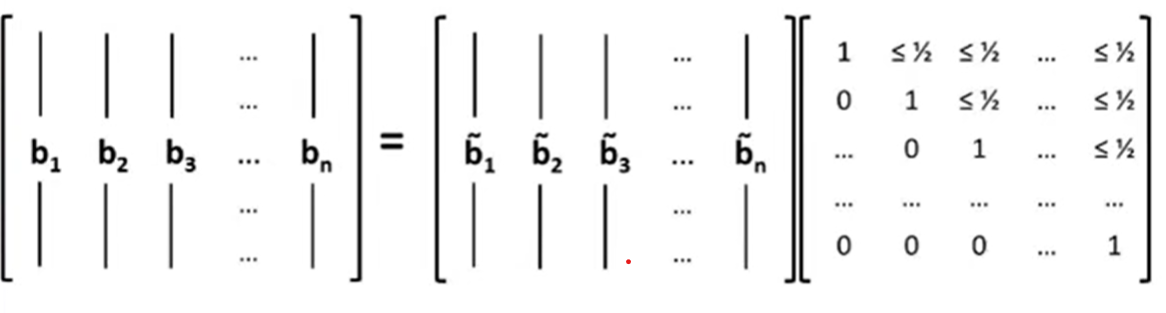
我们有一个基B,用$b_1,b_2,\dots,b_n$表示,写成列向量的形式即得到等号左边的矩阵。
中间的是施密特正交基,用$\widetilde{b}_1,\widetilde{b}_2,\dots,\widetilde{b}_n$表示
需要在正交基乘上右边的矩阵才能得到B
如何让这些u都小于0.5?
只要把每一列多次减去第一列就可以满足
如何保证向量不会减小得太快
如果$\widetilde{b}_2$和$\widetilde{b}_3$不符合第二个条件,会把$\widetilde{b}_2$和$\widetilde{b}_3$换一下
每次交换后,我们都会更接近于得到一个更好的基
这里没给出证明。
一道例题讲解格密码的应用:
入门题
题目:
1 | import gmpy2 |
要拿到flag,就得求出f的值
先令$f’ = f+20192020202120222023$
已知$h \equiv f’^{-1}g (\mod p)$
$\therefore hf’ \equiv g (\mod p)$
$\therefore g = hf’ -kp$
构造出
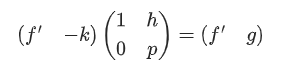
为什么LLL算法可以得到我们需要的f’,g
LLL算法可以把$(h,1),(p,0)$这组基,变成正交化程度最大的一组基,它可以求解最短向量问题
如果说$点(f’,g)$正好是最短向量,那是不是用LLL算法就可以求解出f’,g的值
为什么点$(f’,g)$是最短向量?
Hermite定理给出了最短向量的上界:
$$
||\vec{v}|| \le \sqrt{n}det(\mathcal{L})^{\frac{1}{n}}
$$
对于格$\mathcal{L}$
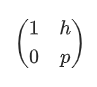
其行列式$det(\mathcal{L})=p$
所以最短向量$||\vec{v}|| \le \sqrt{2p}$
而$p$是$512bit$的,$g$是$128bit$
所以向量$\vec{v}=(f’,g)$的长度$||\vec{v}||$远小于$\sqrt{2p}$的大小
所以可以认为我们需要求的$f’,g$就是最短向量
求解出$f’$后,我们便能求出f
构造的矩阵依赖下式
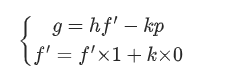
exp:
1 | import libnum |
值得注意的是,当我们把中间的已知矩阵进行乘法以后,输出的结果也会有所不同。
例如,我把中间向量修改为
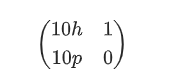
输出的值是原来g的10倍
$$
\because f’×10h-10p×k = 10g
$$
在一定情况下,可以先求需求量的倍数,再求需求量
参考
【精选】高斯启发式Gaussian Heuristic 格理论相关知识-CSDN博客
刘巍然-学酥投稿视频-刘巍然-学酥视频分享-哔哩哔哩视频 (bilibili.com)