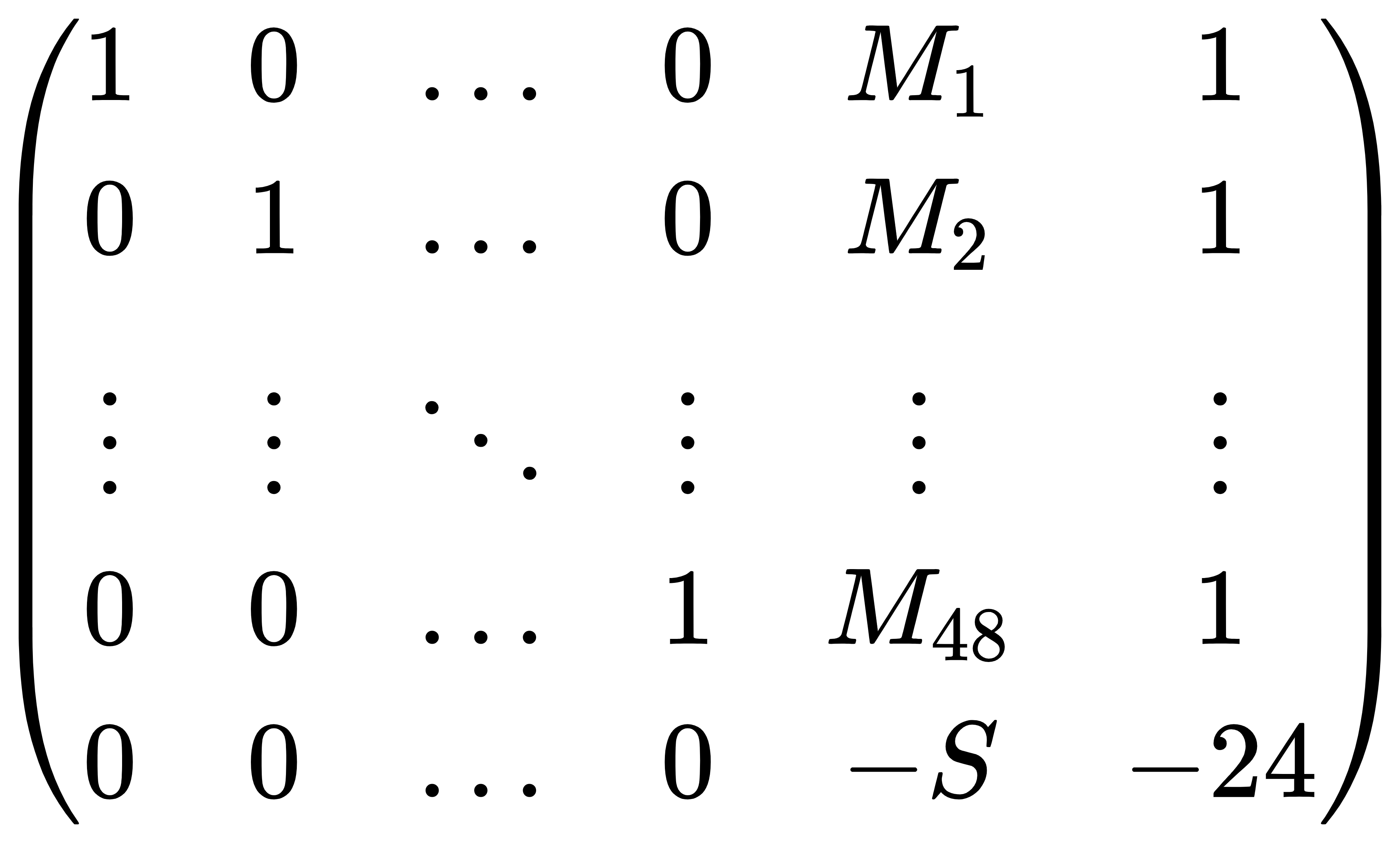2023DASCTF X CBCTF

发表于 更新于 阅读次数： Waline： 本文字数： 1.4k 阅读时长 ≈ 5 分钟

记录2023DASCTF X CBCTF | 无畏者先行————Crypto方向wp

https://test-cuycc6s9lprw.feishu.cn/docx/T7budbiSWoTNd4xQGVicHL1Vnpf

EzRSA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
from Crypto.Util.number import *
import random
from gmpy2 import *
from libnum import *
from flag import flag

def padding(f):
    random_chars = bytes([random.randint(0, 255) for _ in range(32)])
    f = f + random_chars
    return f

def guess_p(p):
    e = 65537
    
    P = p
    n1 = getPrime(512)*getPrime(512)
    with open('enc.txt', 'w+') as f:
        while jacobi(2,n1) == 1:
            n1 = getPrime(512)*getPrime(512)
        while P:
            pad = random.randint(0, 2**2023)**2 
            message = pad << 1 + P % 2
            cipher = pow(message, e, n1)
            f.write(str(cipher)+'n')
            P //= 2
    print("n1 = "+ str(n1) )    
    
def guess_q(q):
    
    def encrypt(q, n):
        e = random.randint(1000,2000)
        noise = random.randint(0, n - 1)
        c = pow(q+noise,e,n)
        return e, noise,c 
    
    n2 = getPrime(512)*getPrime(512)
    e1, noise1, c1 = encrypt(q, n2)
    e2, noise2, c2 = encrypt(q, n2)
    print("n2 = "+ str(n2) ) 
    print('(e1, noise1, c1) =', (e1,noise1,c1))
    print('(e2, noise2, c2) =', (e2,noise2,c2))
p = getPrime(512)
q = getPrime(512)

n = p*q
guess_p(p)
guess_q(q)
e = 0x10001
flag = padding(flag)
m = bytes_to_long(flag)
c = pow(m,e,n)

print("c = " + str(c))
'''
n1 = 65634094430927080732256164808833233563732628654160389042977689628512527168256899310662239009610512772020503283842588142453533499954947692968978190310627721338357432052800695091789711809256924541784954080619073213358228083200846540676931341013554634493581962527475555869292091755676130810562421465063412235309
n2 = 103670293685965841863872863719573676572683187403862749665555450164387906552249974071743238931253290278574192713467491802940810851806104430306195931179902098180199167945649526235613636163362672777298968943319216325949503045377100235181706964846408396946496139224344270391027205106691880999410424150216806861393
(e1, noise1, c1) = (1743, 44560588075773853612820227436439937514195680734214431948441190347878274184937952381785302837541202705212687700521129385632776241537669208088777729355349833215443048466316517110778502508209433792603420158786772339233397583637570006255153020675167597396958251208681121668808253767520416175569161674463861719776, 65643009354198075182587766550521107063140340983433852821580802983736094225036497335607400197479623208915379722646955329855681601551282788854644359967909570360251550766970054185510197999091645907461580987639650262519866292285164258262387411847857812391136042309550813795587776534035784065962779853621152905983)
(e2, noise2, c2) = (1325, 35282006599813744140721262875292395887558561517759721467291789696459426702600397172655624765281531167221787036009507833425145071265739486735993631460189629709591456017092661028839951392247601628468621576100035700437892164435424035004463142959219067199451575338270613300215815894328788753564798153516122567683, 50327632090778183759544755226710110702046850880299488259739672542025916422119065179822210884622225945376465802069464782311211031263046593145733701591371950349735709553105217501410716570601397725812709771348772095131473415552527749452347866778401205442409443726952960806789526845194216490544108773715759733714)
c = 124349762993424531697403299350944207725577290992189948388824124986066269514204313888980321088629462472088631052329128042837153718129149149661961926557818023704330462282009415874674794190206220980118413541269327644472633791532767765585035518183177197863522573410860341245613331398610013697803459403446614221369
'''

求解q用了相关消息的考点

$\because c_1 \equiv (q + noise_1)^{e_1} \mod n_2$，$c_2 \equiv (q+noise_2)^{e_2} \mod n_2$

q是$c_1 \equiv (x + noise_1)^{e_1} \mod n_2$和$c_2 \equiv (x+noise_2)^{e_2} \mod n_2$这两个多项式的公共根

所以两个多项式有公因式$(x-q)$，gcd即可求得$(x-q)$，进而求得q

求解p需要用到雅可比符号的知识点

雅可比符号：

基础数论学习笔记（17）- Legendre Symbol 勒让德符号 - 知乎 (zhihu.com)这篇文章中讲了如何计算雅可比符号

雅可比符号$(\frac{a}{pi})$的作用是判断$a$是否是模$pi$下的二次剩余，若勒让德符号值为1则是二次剩余，为-1则是二次非剩余。

雅可比符号的完全积性

完全积性指的是$(\frac{ab}{p}) = (\frac{a}{p})(\frac{b}{p}) $

1
2
while jacobi(2,n1) == 1:
	n1 = getPrime(512)*getPrime(512)

第一个while，保证了$(\frac{2}{n_1}) \ne 1$

$\because (\frac{2}{n_1}) = (\frac{2}{p_1})(\frac{2}{q_1}) \ne 1$

所以$2$不能同为$p_1$、$q_1$的二次剩余或二次非剩余，而必须是其中一个的二次剩余，是另一个的二次非剩余。

说明：把random.randint(0, 2**2023)当作$pad$,所以后面出现的是$pad^2$

第二个while内部的过程为

message = pad << 1 + P % 2等同于$message = pad^2 << (1 + P_{lastbit})$

$ciher \equiv message^e \mod n_1$

利用雅可比符号的完全可乘性

我们得到$(\frac{cipher}{n_1}) = (\frac{message^e}{n_1}) = (\frac{message}{n_1})^e$(第二个等号可以看为e次雅可比符号相乘)

因为e是一个奇数，因此无论是-1还是1都会保持原值，也就有：
$$
(\frac{cipher}{n_1}) = (\frac{message}{n_1})^e = (\frac{message}{n_1})
$$
下面分两种情况进行分析

情况1：P当前的最低位为0

如果P当前的最低位为0，就有$message = pad^2 << 1 = 2 \times pad^2$

于是，有$(\frac{message}{n_1}) = (\frac{2\times pad^2}{n_1}) = (\frac{2}{n_1})(\frac{pad^2}{n_1})$

$\because (\frac{2}{n_1}) =(-1)^{\frac{n_1^2 - 1}{8}} = -1$

$\therefore (\frac{message}{n_1}) = (\frac{2\times pad^2}{n_1}) = (\frac{2}{n_1})(\frac{pad^2}{n_1}) = -1\times (\frac{pad^2}{p_1})(\frac{pad^2}{q_1})$

根据定理，因为$p_1$是素数，所以$(pad,p_1) = 1$，则$(\frac{pad^2}{p_1}) = 1$，同理$(\frac{pad^2}{q_1}) = 1$

所以当P的该位为0时，计算出的雅可比符号值为-1

情况2：P当前的最低位为1

当P当前的最低位为1时，有$message = pad^2 << 2 = 4\times pad^2$

于是，有$(\frac{message}{n_1}) = (\frac{4\times pad^2}{n_1}) = (\frac{4\times pad^2}{p_1})(\frac{4\times pad^2}{q_1}) = (\frac{4}{p_1})(\frac{pad^2}{p_1})(\frac{4}{q_1})(\frac{pad^2}{q_1})$

根据定理，因为$p_1$是素数，所以$(2,p_1)=1,(pad,p_1) = 1$，则$(\frac{4}{p_1})= 1,(\frac{pad^2}{p_1}) = 1$，同理$(\frac{4}{q_1})= 1,(\frac{pad^2}{q_1}) = 1$

所以$(\frac{cipher}{n_1}) = (\frac{message}{n_1}) = 1$

所以当P的该位为1时，计算出的雅可比符号值为1

因此我们可以把这个作为依据来还原P的每一个比特位，从而还原p

exp:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# sage
from gmpy2 import *
from libnum import *
from Crypto.Util.number import *

e = 
n1 = 
n2 = 
(e1, noise1, c1) = (, , )
(e2, noise2, c2) = (, , )
c = 
f = open("enc.txt",'r').read()
cipher = f.split('n')
cipher = cipher[:-1]

def get_p(cipher):
    p = ""
    for i in cipher:
        if jacobi(int(i),n1) == 1:
            p += '1'
        else:
            p += '0'
    p = int(p[::-1],2)
    return p

def gcd(g1, g2):
    while g2:
        g1, g2 = g2, g1 % g2
    return g1.monic()
def get_q(n,e1,e2,c1,c2):
    PR.<x> = PolynomialRing(Zmod(n))
    g1 = (x + noise1)^e1 - c1
    g2 = (x + noise2)^e2 - c2
    return -gcd(g1, g2)[0]

p = get_p(cipher)
print(isPrime(p))
# print(p)
q = get_q(n2,e1,e2,c1,c2)
# print(q)

p = 9473204278465588641589315677772678997836862033858760337441231265335880892205102590571357305720744128962068300763212493598006400853597404586755248901932203
q = 13189337905641321257372188436353844418280745284875462357019668708167547026960641869513283218672677712590326347601424108528959315675307896082223561007980457
phi = (p-1) * (q-1)
n = p * q
d = gmpy2.invert(e,phi)
m = pow(c,d,n)
print(long_to_bytes(int(m)))
# DASCTF{W05-y03r_m2st1r-j2c0b1_2nd_p01yn0mi2l!}

Backpack

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from random import shuffle

def gen_e():
    e = []
    for i in range(8):
        ee = [0]*3+[1]*3
        shuffle(ee)
        e += ee
    return e
    
e = gen_e()
nbit = len(e)
flag = 'DASCTF{'+sha256(''.join([str(i) for i in e]).encode()).hexdigest()+'}'

a = [randint(1,2^nbit) for i in range(nbit)]

re = 0
for i in range(nbit):
    re += e[i]*a[i]

print(a)
print(re)

背包加密，但是密度$\frac{len(M)}{max(M_i)} > 0.9408$

常规的格解不出来

利用上48个$e_i$中，有24个1，即$\sum_{i=1}^{48}e_i = 24$，给格多加上一列进行规约，判断最后两个数为0

构造：

但其实解题的时候，要在最后两列乘上一个比较大的数，我这里取$K=2^{10}$

exp:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# sage
from hashlib import sha256
M = [...]
S = 

n = len(M)
K = 2^10

Ge = Matrix(ZZ,n+1,n+2)
for i in range(n):
    Ge[i,i] = 1
    Ge[i,n] = K*M[i]
Ge[n,n] = -K*S

for i in range(n):
    Ge[i,n+1] = K
Ge[n,n+1] = -24 * K

for line in Ge.LLL():
    if line[-1] == 0 and line[-2] == 0:
        x = [abs(i) for i in line[:-2]]
        if set(x).issubset([0, 1]):
            print(x)
            flag = 'DASCTF{'+sha256(''.join([str(i) for i in x]).encode()).hexdigest()+'}'
            print(flag)

set(x).issubset([0, 1])：先把x转成集合，再判断x是否为[0,1]的子集

最后会得到两个结果，分别是DASCTF{b2eeee766ce525a62eaaba8db0c5c5246d5abf10e15526258f8cc3f6631e375f}

DASCTF{22a53e95a21f1000ac5dcc618f67586c412e1072f5bb1fee0ee5ce3d1794e3f3}

正确的是DASCTF{22a53e95a21f1000ac5dcc618f67586c412e1072f5bb1fee0ee5ce3d1794e3f3}

-------------已经到底啦！-------------