2023ISCTF

发表于 2023-11-29 更新于 2023-12-05 分类于 Wp 阅读次数： Waline：本文字数： 11k 阅读时长 ≈ 41 分钟

2023ISCTF——Crypto题解

Crypto

easy_rsa

rsa_d

上面两题p,q都给了，白给啦

七七的欧拉

$n = p^8$，计算$\phi(n) = p^7\times(p-1)$

exp:

from Crypto.Util.number import *
import gmpy2

e=
n=
c=

p = 
phi = p**7*(p-1)
d = gmpy2.invert(e,phi)
m = pow(c,d,n)
print(long_to_bytes(m))
# ISCTF{3237saq-21se82-3s74f8-8h84ps7-9qw45v7-6bs531-s26h23-c7iu01}

夹里夹气

嘤嘤？嘤嘤？ 嘤嘤？嘤嘤？嘤嘤？ 嘤嘤嘤嘤嘤？嘤嘤嘤嘤嘤？ 嘤嘤嘤 嘤嘤？嘤嘤？嘤嘤嘤嘤嘤？ 嘤嘤嘤嘤嘤嘤嘤嘤嘤嘤嘤嘤嘤嘤？嘤嘤嘤嘤嘤嘤 嘤嘤？嘤嘤？嘤嘤？嘤嘤？ 嘤嘤？嘤嘤？嘤嘤？ 嘤嘤嘤嘤嘤？嘤嘤？嘤嘤？ 嘤嘤嘤嘤嘤？嘤嘤？ 嘤嘤？嘤嘤？嘤嘤？嘤嘤？ 嘤嘤？嘤嘤？嘤嘤嘤嘤嘤嘤嘤嘤？嘤嘤嘤 嘤嘤？嘤嘤？嘤嘤？ 嘤嘤？嘤嘤？嘤嘤嘤嘤嘤？ 嘤嘤？嘤嘤嘤嘤嘤嘤嘤嘤嘤 嘤嘤？嘤嘤？嘤嘤嘤嘤嘤嘤嘤嘤？嘤嘤嘤 嘤嘤？嘤嘤嘤嘤嘤嘤嘤嘤嘤 嘤嘤嘤嘤嘤？嘤嘤？ 嘤嘤嘤嘤嘤？ 嘤嘤？嘤嘤？嘤嘤嘤嘤嘤？ 嘤嘤？嘤嘤嘤嘤嘤嘤嘤嘤嘤 嘤嘤？嘤嘤？嘤嘤嘤嘤嘤嘤嘤嘤？嘤嘤嘤 嘤嘤嘤嘤嘤？嘤嘤？ 嘤嘤？嘤嘤嘤嘤嘤嘤嘤嘤嘤 嘤嘤嘤嘤嘤？ 嘤嘤？嘤嘤？嘤嘤嘤嘤嘤？ 嘤嘤？嘤嘤嘤嘤嘤嘤嘤嘤嘤 嘤嘤嘤嘤嘤？嘤嘤？ 嘤嘤嘤嘤嘤嘤 嘤嘤嘤嘤嘤嘤嘤嘤嘤嘤嘤嘤嘤嘤嘤嘤嘤？嘤嘤嘤

嘤嘤？换.，嘤嘤嘤换-

1zRSA

from secret import flag
from Crypto.Util.number import *
import gmpy2

e = 65537
def genKey(nbits):
    while 1:
        p1 = getPrime(3*nbits)
        p2 = gmpy2.next_prime(p1)
        q1 = getPrime(nbits)
        q2 = getPrime(nbits)
        if (abs((p1 - p2)*q1*q2 / p2) < 0.5):
            n1 = p1 * q1
            n2 = p2 * q2
            return n1,n2

def encrypt(message,e,n):
    m = bytes_to_long(message)
    cipher = pow(m,e,n)
    return cipher

e = 65537
nbits = 512
N1,N2 = genKey(nbits)
c = encrypt(flag,e,N1)

print("c =",c)
print("N1 =",N1)
print("N2 =",N2)

"""
c = 10514867898770499427284608506159580569755258729683776720082395249877529851029152305989048383470182992945743997295638334301128554841767619528809377736651238576700664675871769469687466885347209033023021132575700436470105289467423655742323143373578268184141573237433927498143740155552829633601489926767185335051352605346248971754473960051955670785777007641909166041398566067524811394639822575661469340152913706417365065683835945980239268665146900957692685590242386540944646586739158427428484471978559453954674292300496568823382513505511940062159025700312492163454304120916055466108498000990408937265075788135466153131436
N1 = 29306627985861300819651846356448043523015086509329909246911330574896611830331438353458702041787309531570626136669100576501108581024502570212983369979387658041578384466200573362881060761873478590684611265249166591510948597798713864127744488747451815919677861684787135464097885906630772472111899455047125676738720391327331161464894360886214160668909531050207033060523194208723151015702926842472554933849380343375654696115359960495727909221926251630408376527033291123026893207722440649867394971680316008434251667567174806214522621693042164997381729300075394393372808917061813346794422821819494227772694592990703688149467
N2 = 18405525902524887428651801489049128242565457677879715229456940729064725933277139190670749899959483734341103740185991771024797037242681566772189045321838652668819112989587974866361063424698215713773139281840970499871668796770682692589505769008516630604297570518689639885716307469568821629424402742264467677407820449195383921766157185602677665872353099155904715047452319853202981674101731121033360393547940246101864940155160699277417096395998766928213545196492031975135121409309520198853066288180944871441224241681478164494169741263236267316380581883196836731872676312125837497320438964940186318916950049777255612191899
"""

根据勒让德理论，题目中已经保证了$|\frac{N_1}{N_2} - \frac{q_1}{q_2}| < \frac{1}{2q_2^2}$即$\frac{(p_1-p_2)q_1q_2}{p_2} < \frac{1}{2}$，所以$\frac{q_1}{q_2}$是$\frac{N_1}{N_2}$的收敛子

连分数展开即可求得$q_1$,$q_2$

exp:

# sage
from Crypto.Util.number import *
import gmpy2

c = 10514867898770499427284608506159580569755258729683776720082395249877529851029152305989048383470182992945743997295638334301128554841767619528809377736651238576700664675871769469687466885347209033023021132575700436470105289467423655742323143373578268184141573237433927498143740155552829633601489926767185335051352605346248971754473960051955670785777007641909166041398566067524811394639822575661469340152913706417365065683835945980239268665146900957692685590242386540944646586739158427428484471978559453954674292300496568823382513505511940062159025700312492163454304120916055466108498000990408937265075788135466153131436
N1 = 29306627985861300819651846356448043523015086509329909246911330574896611830331438353458702041787309531570626136669100576501108581024502570212983369979387658041578384466200573362881060761873478590684611265249166591510948597798713864127744488747451815919677861684787135464097885906630772472111899455047125676738720391327331161464894360886214160668909531050207033060523194208723151015702926842472554933849380343375654696115359960495727909221926251630408376527033291123026893207722440649867394971680316008434251667567174806214522621693042164997381729300075394393372808917061813346794422821819494227772694592990703688149467
N2 = 18405525902524887428651801489049128242565457677879715229456940729064725933277139190670749899959483734341103740185991771024797037242681566772189045321838652668819112989587974866361063424698215713773139281840970499871668796770682692589505769008516630604297570518689639885716307469568821629424402742264467677407820449195383921766157185602677665872353099155904715047452319853202981674101731121033360393547940246101864940155160699277417096395998766928213545196492031975135121409309520198853066288180944871441224241681478164494169741263236267316380581883196836731872676312125837497320438964940186318916950049777255612191899
e = 65537
cf = continued_fraction(Integer(N1) / Integer(N2))
i = 1
while 1:
    q1 = cf.numerator(i)
    q2 = cf.denominator(i)
    if N1 % q1 == 0 and q1 != 1:
        print(q1)
        p1 = N1 // q1
        d = gmpy2.invert(e,(p1-1)*(q1-1))
        m = pow(c,d,N1)
        flag = long_to_bytes(int(m))
        if b"ISCTF" in flag:
            print(flag)
            break
        
    i += 1
# ISCTF{6f3af9a9-2727-4d48-afb4-9ca82de893f3}

from Crypto.Util.number import *
from secret import flag

def genKey(nbits):
    p = getPrime(nbits)
    q = getPrime(nbits)
    
    N = p*p*q
    d = inverse(N, (p-1)*(q-1)//GCD(p-1, q-1))
    return N,d

def encrypt(message,N):
    m = bytes_to_long(flag)
    c = pow(m, N, N)
    return c

nbits = 1024
m = bytes_to_long(flag)
N,d = genKey(nbits)
c = encrypt(m,N)

print('c =', c)
print('N =', N)
print('d =', d)

"""
c = 29897791365314067508830838449733707533227957127276785142837008063510003132596050393885548439564070678838696563164574990811756434599732001622138564176327233154381380717648392357672642893142367607369679906940371540867456654151408884171467638060523066406441697453971996011548195499549200103123841556085936672833238264876038160712793697159776332101536779874757463509294968879216810485825310481778472384531442206034564488532399171243463881900578407746982324779260941957792455217641883334131366614310644607114128868153897806362954456585661855569432513785225453501792356175649676419772626548071916379318631677869452985829916084336045071072493567871623113923140668031380684940109024609167449291380675124701557542736834722898328082888430566229322840781411336263268594978558564310744076581639469210462567543585251718744340216155557606004995449505782302864725856877289388008819135023371948017425832082773421030256964953984562211638060
N = 3231913372897424708803097969843687520868057190788284975066875241636436021279559026753076528399891936983240045179193386905918743759145596242896507856007669217275515235051689758768735530529408948098860529277921046146065473333357110158008648799207873976745048714516868561754202543130629713461365314627535982379718931633528922076268531363809414255082933615667770491818402126891370106045838695484124212397783571579791558324350069782623908757815983802849109451590357380624488436968737140312471089662428308113246310588336044438265822574558816510054763215983649467009345458480077882624118620789015758507736272402998721366662352794082495441303895025585316667229865533166614969641012195668280586477033200418153345241668242651407009849656745509386158276185301334443855737552801531617549980843398648751032649895403939319648954908487619711555700124294191702406981128355348449748466449951568451135718146828444185238617155432417897711198169
d = 220908195398117048628110042133057032501548264225985823161565460390793825899523662424732910718579350524590368287207857059670558852106434615134645183432670023784725430385048028248108677670095524205518013647694485975996499747580966911259433184798952372110628624294686853944766950244209186984164963987120416687012811346656498861438432610431705868541829977481875385468143747334359481673214618931159403123892213161430602430294790913847722073762999311674428134241956293914716183107414340330449465142849402354034926378025006749405210014879947411570380433942279355488861684317611066949685697268714760755591128598654573304969
"""

考察Schmidt-Samoa密码系统

$\because Nd \equiv 1\mod (p-1)(q-1)$

任意选取一个$a$，有$a^{Nd}\equiv a^{k(p-1)(q-1) + 1} \equiv a \mod pq$

$\therefore k\times (p\times q) = a^{Nd} - a$

和$N$求公因数即可得到$p\times q$，再用d解密即可

exp:

import gmpy2

c = 29897791365314067508830838449733707533227957127276785142837008063510003132596050393885548439564070678838696563164574990811756434599732001622138564176327233154381380717648392357672642893142367607369679906940371540867456654151408884171467638060523066406441697453971996011548195499549200103123841556085936672833238264876038160712793697159776332101536779874757463509294968879216810485825310481778472384531442206034564488532399171243463881900578407746982324779260941957792455217641883334131366614310644607114128868153897806362954456585661855569432513785225453501792356175649676419772626548071916379318631677869452985829916084336045071072493567871623113923140668031380684940109024609167449291380675124701557542736834722898328082888430566229322840781411336263268594978558564310744076581639469210462567543585251718744340216155557606004995449505782302864725856877289388008819135023371948017425832082773421030256964953984562211638060
N = 3231913372897424708803097969843687520868057190788284975066875241636436021279559026753076528399891936983240045179193386905918743759145596242896507856007669217275515235051689758768735530529408948098860529277921046146065473333357110158008648799207873976745048714516868561754202543130629713461365314627535982379718931633528922076268531363809414255082933615667770491818402126891370106045838695484124212397783571579791558324350069782623908757815983802849109451590357380624488436968737140312471089662428308113246310588336044438265822574558816510054763215983649467009345458480077882624118620789015758507736272402998721366662352794082495441303895025585316667229865533166614969641012195668280586477033200418153345241668242651407009849656745509386158276185301334443855737552801531617549980843398648751032649895403939319648954908487619711555700124294191702406981128355348449748466449951568451135718146828444185238617155432417897711198169
d = 220908195398117048628110042133057032501548264225985823161565460390793825899523662424732910718579350524590368287207857059670558852106434615134645183432670023784725430385048028248108677670095524205518013647694485975996499747580966911259433184798952372110628624294686853944766950244209186984164963987120416687012811346656498861438432610431705868541829977481875385468143747334359481673214618931159403123892213161430602430294790913847722073762999311674428134241956293914716183107414340330449465142849402354034926378025006749405210014879947411570380433942279355488861684317611066949685697268714760755591128598654573304969

tmp = pow(2,d*N,N) - 2
pq = gmpy2.gcd(tmp,N)

m = pow(c,d,pq)
print(bytes.fromhex(hex(m)[2:]))
# ISCTF{aeb8be10-ff19-42cf-8cfd-2ce71ac418e8}

EasyAES

from secret import flag,key
from Crypto.Util.number import *
from Crypto.Cipher import AES
import os

assert(len(flag)==39)
assert(len(key)==16)

def padding(msg):
    tmp = 16 - len(msg)%16
    pad = hex(tmp)[2:].zfill(2)
    return bytes.fromhex(pad*tmp)+msg

def encrypt(message,key,iv):
    aes = AES.new(key,AES.MODE_CBC,iv=iv)
    enc = aes.encrypt(message)
    return enc

iv = os.urandom(16)
message = padding(flag)
hint = bytes_to_long(key)^bytes_to_long(message[:16])
enc = encrypt(message,key,iv)

print(enc)
print(hex(hint))

"""
b'bsF\xb6m\xcf\x94\x9fg1\xfaxG\xd4\xa3\x04\xfb\x9c\xac\xed\xbe\xc4\xc0\xb5\x899|u\xbf9e\xe0\xa6\xdb5\xa8x\x84\x95(\xc6\x18\xfe\x07\x88\x02\xe1v'
0x47405a4847405a48470000021a0f2870
"""

padding函数是在明文前面填充\t\t\t\t\t\t\t\t\t

再根据flag开头是ISCTF{

再利用CBC加密的特性，爆破最后key的最后一位以及iv即可求解

exp:

from Crypto.Util.number import *
from Crypto.Cipher import AES
import os

def padding(msg):
    tmp = 16 - len(msg)%16
    pad = hex(tmp)[2:].zfill(2)
    return bytes.fromhex(pad*tmp)+msg

hint = 0x47405a4847405a48470000021a0f2870

c = b'bsF\xb6m\xcf\x94\x9fg1\xfaxG\xd4\xa3\x04\xfb\x9c\xac\xed\xbe\xc4\xc0\xb5\x899|u\xbf9e\xe0\xa6\xdb5\xa8x\x84\x95(\xc6\x18\xfe\x07\x88\x02\xe1v'

m = b"\t\t\t\t\t\t\t\t\tISCTF{"
for i in range(256):
    try:
        msg = m + long_to_bytes(i)
        key = long_to_bytes(hint ^ bytes_to_long(msg))
        c0 = c[:16]
        aes = AES.new(key,AES.MODE_ECB)
        cc = aes.decrypt(c0)
        iv = long_to_bytes(bytes_to_long(cc) ^ bytes_to_long(msg))
        
        d = AES.new(key,AES.MODE_CBC,iv = iv)
        flag = d.decrypt(c)
        if (b"ISCTF{" in flag) and (flag[-1] == 125):
            print(flag) 
        else:
            pass
    except:
            pass
                # ISCTF{1b106cea3fb848e7bea310c9851f15c1}

ezRSA

from secret import flag,key
from Crypto.Util.number import *
from random import randint,getrandbits
from sympy import factorial as factor
from gmpy2 import is_prime as is_strongPrime
from gmpy2 import gcd
from libnum import s2n

def step1(m):
	p,q = getPrime(1024),getPrime(1024)
	n=p*q
	e=getPrime(512)
	phi = (p-1)*(q-1)
	while gcd(e,phi) != 1:
		e=getPrime(512)
	d = pow(e,-1,phi)
	k = randint(800,1500)
	f = factor(k)
	# print(f"\n\n\n\n{k=}\n\n\n\n")
	leak = (pow(e, 2) + (e*d - 1)*f)*getPrime(256) + k
	print(f"{n=}")
	print(f"{leak=}")
	e = 65537
	c = pow(m,e,n)
	return c


def step2(m):
	#the key number is three part 
	assert key < 10**9
	assert (is_prime(key) and not is_strongPrime(key))

	p,q = getPrime(512),getPrime(512)
	n=p*q
	leak1 = pow(p,q,n) + pow(q,p,n)
	print(f"{n=}")
	print(f"{leak1=}")
	e=0x10001
	c = pow(m,e,n)
	seed = getrandbits(64)
	a = getPrime(256)
	b = getPrime(256)
	leak2 = []
	for i in range(10):
		leak2.append(seed := (seed * a + b) % p)
	print(f"{leak2 = }")
	seed = (seed * a + b) % p
	base = key ^ seed
	final = []
	while c > 0:
		final.append(c % base)
		c //= base

	return final


# def most(lis):
# 	return lis.count(True) > lis.count(False)

def is_prime(p):
	check = [2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97]
	return all([pow(i,p-1,p)==1 for i in check])


def main():
	assert len(flag) == 2
	print("step1:")
	print("c =",step1(s2n(flag[0])))
	print("step2:")
	print("final =",step2(s2n(flag[1])))

if __name__ == "__main__":
	main()

Part1

设getPrime(256) = a

$$
\because leak = (e^2 + (ed-1)\times k!)a + k
$$
$$
即leak = ae^2 + (ed-1)\times k!\times a + k
$$

$$
\therefore leak -k = ae^2 + (ed-1)\times k!\times a
$$

因为$k!$非常大

如果用leak - k模掉k!，得到的结果就只剩下了$ae^2$

如果用leak - k模掉(k + 1)!，得到的结果肯定是大于$ae^2$

判断最后的结果是否和$ae^2$为一个数量级，就能求出$k$

求出$k$之后，我们就能求得$a\times(ed-1) = t\times \phi(n)$

用$t\phi(n)$代替$\phi(n)$就可以求得$d$了

part2

$leak \equiv p^q\mod n + q^p \mod n$

把模缩小

$leak \equiv p^q \mod q + q^p \mod p$

由费马小定理得

$leak \equiv p +q$，联立$n = p\times q$，解方程求得$p,q$

其实$p$可以在lcg中求

下面是求解LCG得到$seed$

最关键在于$key$

$key$实际上是一个为素数，根据题目给的

1
2
3

def is_prime(p):
	check = [2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97]
	return all([pow(i,p-1,p)==1 for i in check])

如果以这个代码来爆破$key$的话，速度太慢了

只要把函数修改为

1
2
3

def is_prime(p):
	check = [2]
	return all([pow(i,p-1,p)==1 for i in check])

原因是，满足$2^{p-1} \equiv 1 \mod p$，$3^{p-1}\equiv 1\mod p$，……，$97^{p-1}\equiv 1\mod p$的数，一定满足，$2^{p-1}\equiv 1 \mod p$

修改后的函数相当于求的是原来集合的母集

然后遍历母集中的元素即可找到$key$

另外可以查卡迈尔数的表oeis.org/A002997/b002997.txt

exp：

from tqdm import *
from Crypto.Util.number import *
from sympy import factorial as factor
import gmpy2
from sympy import symbols,solve
from gmpy2 import is_prime as is_strongPrime

def findpq(n,leak):
    p = symbols('p')
    q = symbols('q')

    eq1 = p + q - leak
    eq2 = p * q - n

    solution = solve((eq1,eq2),(p,q))
    for i in solution:
        p = int(i[0])
        if n % p == 0:
            q = n // p
            return p,q

def findseed(output,p):
    p1 = output[-1]-output[-2]
    p2 = output[-2]-output[-3]
    Ani = gmpy2.invert(p2,p)
    a = p1 * Ani % p
    b = (output[-1] - a*output[-2]) % p
    seed = (output[-1] * a + b) % p
    return seed

def findk(leak):
    for k in range(800,1500):
        f = factor(k)
        tmp = (leak - k) % f
        if int(tmp).bit_length() > 1280:
            return k-1

def decrypt1(leak,n,c):
    k = findk(leak)
    #print(k)
    #1039
    f = factor(k)
    tmp = (leak - k) % f
    kphi = (leak - k - tmp) // f
    d = gmpy2.invert(65537,gmpy2.mpz(kphi))
    flag1 = long_to_bytes(pow(c,d,n))
    return flag1

def decrypt2(seed,cipher,KEY,d):
    for key in tqdm(KEY):
        c = 0
        base = key ^ seed
        for i in range(len(cipher)):
            c += cipher[i] * (base ** i)
            m = pow(c,d,n)
            flag = long_to_bytes(m)
            if chr(flag[-1]) == "}":
                print("key=",key)
                #56052361
                print(flag)

n=
leak=
c = 
flag1 = decrypt1(leak,n,c)

n = 
leak1 = 
p,q = findpq(n,leak1)
d = gmpy2.invert(65537,(p-1)*(q-1))
leak2 = [...]
final = [...]
seed = findseed(leak2,p)
# seed = 4200187646212318518523978419030779663356898929497560679154263632881543657050959427183966634462102477814580819864753365867968297383142555109096365631733722
KEY = [...]
# decrypt2(seed,final,KEY,d)
flag2 = b"_LCG_also_like_Carmichael_number}"

print(flag1+flag2)
#ISCTF{yOu_kn0W_RSAgcd_and_g0Od_at_LCG_also_like_Carmichael_number}

baby group

学艺不精，理解了好几个晚上才理解 >ᯅ<

task.py

from Per import P,Block
from secret import flag
import hashlib
from libnum import s2n

mask = P(256)

print(mask**2)
mask_hash = hashlib.sha512(str(mask).encode()).hexdigest()
print("the mask hash is:" + mask_hash)

mul = P(256)
print(f"{mul=}")
temp = hashlib.sha512(str(mask * mul).encode()).hexdigest()

msg = s2n(flag) ^ int(temp,16)

worker = Block()
print(f"pubkey(q,h):{worker.getPublicKey()}")
c = worker.enc(msg)
print(f"{c=}")
dec = worker.dec(c)

Per.py

import random
from gmpy2 import invert,sqrt,gcd

class P:
	def __init__(self, data):
		if type(data) is int:
			self.size = data
			self._list = [i+1 for i in range(self.size)]
			self._initialize()			
		elif type(data) is list:
			self._list = data
			self.size = len(self._list)

	def __mul__(self, other):
		return P(self._iterList(self.getList(),other.getList()))

	def __repr__(self):
		return str(self._list)

	def __len__(self):
		return len(self._list)

	def __pow__(self, other):
		tempList = self._list
		for _ in range(1,other):
			tempList = self._iterList(tempList, tempList)
		return P(tempList)

	def __str__(self):
		return str(self._list)

	def getList(self):
		return self._list

	def _initialize(self):
		for i in range(10):
			random.shuffle(self._list)

	def _iterList(self, List1,List2):
		new_list = []
		for elem in List1:
			new_list.append(List2[elem - 1])
		return new_list

pass

class Block():
	def __init__(self):
		while True:
			self.q = random.getrandbits(2048)
			self.f = random.randint(1, sqrt(self.q // 2))
			self.g = random.randint(sqrt(self.q // 4), sqrt(self.q // 2))
			if gcd(self.f, self.q * self.g) == 1:
				break

		self.h = invert(self.f, self.q) * self.g % self.q
		
	def getPublicKey(self):
		return (int(self.q), int(self.h))
	
	def enc(self, m):
		assert m < sqrt(self.q//4)
		r = random.randint(1, sqrt(self.q // 2))
		e = (r * self.h + m) % self.q
		
		return int(e)

	def dec(self, e):
		a = self.f * e % self.q
		b = invert(self.f, self.g) * a % self.g
		return b

output

[82, 237, 32, 83, 30, 200, 116, 114, 4, 147, 171, 152, 193, 19, 170, 136, 186, 8, 124, 159, 225, 6, 180, 125, 74, 14, 255, 60, 187, 132, 222, 121, 56, 79, 57, 229, 87, 27, 72, 197, 201, 191, 75, 38, 135, 177, 165, 149, 17, 172, 173, 59, 210, 108, 31, 142, 163, 227, 178, 226, 73, 256, 190, 12, 103, 238, 129, 157, 219, 131, 67, 28, 68, 236, 168, 209, 245, 93, 61, 122, 208, 137, 49, 94, 111, 18, 161, 106, 54, 175, 70, 16, 110, 5, 218, 81, 233, 45, 91, 188, 151, 104, 148, 184, 228, 248, 150, 176, 167, 35, 130, 242, 126, 156, 42, 169, 232, 102, 50, 214, 179, 205, 9, 235, 97, 84, 246, 36, 76, 240, 52, 144, 98, 86, 99, 21, 64, 217, 15, 202, 206, 55, 244, 65, 23, 53, 250, 78, 22, 215, 25, 66, 143, 107, 195, 80, 196, 254, 174, 33, 162, 252, 141, 153, 43, 185, 211, 220, 115, 127, 216, 251, 139, 95, 146, 48, 239, 241, 37, 199, 13, 160, 90, 223, 123, 181, 120, 164, 118, 112, 128, 192, 249, 39, 2, 207, 71, 182, 145, 62, 3, 92, 183, 194, 100, 24, 133, 10, 117, 234, 29, 11, 140, 166, 85, 224, 230, 134, 189, 63, 46, 58, 231, 247, 47, 154, 44, 77, 89, 101, 69, 40, 26, 243, 253, 41, 51, 105, 155, 138, 1, 212, 20, 203, 213, 198, 158, 88, 109, 34, 119, 221, 113, 96, 204, 7]

the mask hash is:91881f508f08fbafec1a6879fc3a1f215135c94c78f03fae8534d54dc05bd4a122a4e4508d32b9e02be08fbbb42a9e3335fc433c20e2da2e012d11b7324f6952

mul=[114, 189, 92, 56, 252, 161, 202, 250, 131, 9, 111, 226, 223, 24, 14, 6, 99, 208, 195, 216, 141, 116, 167, 34, 5, 129, 15, 158, 178, 197, 4, 187, 27, 200, 144, 76, 74, 154, 86, 249, 93, 112, 46, 104, 25, 248, 40, 225, 38, 98, 186, 169, 64, 118, 33, 88, 26, 106, 183, 43, 201, 198, 242, 135, 110, 218, 244, 120, 83, 212, 192, 185, 148, 142, 11, 45, 232, 107, 18, 170, 60, 130, 247, 67, 65, 211, 182, 213, 134, 254, 70, 191, 210, 176, 145, 217, 82, 229, 125, 193, 155, 41, 113, 103, 49, 231, 133, 75, 109, 238, 126, 245, 163, 233, 227, 181, 51, 12, 143, 234, 239, 59, 240, 209, 42, 205, 230, 253, 203, 219, 23, 136, 32, 87, 102, 94, 85, 62, 172, 236, 124, 100, 256, 196, 50, 101, 206, 150, 89, 29, 61, 69, 246, 237, 16, 37, 184, 90, 162, 22, 36, 10, 31, 52, 190, 17, 55, 115, 251, 77, 214, 122, 1, 255, 151, 157, 241, 224, 3, 44, 48, 175, 194, 138, 179, 159, 160, 53, 80, 73, 8, 35, 156, 117, 58, 140, 221, 180, 72, 123, 147, 95, 228, 97, 71, 204, 39, 149, 2, 19, 173, 139, 146, 54, 96, 220, 79, 66, 57, 127, 243, 188, 165, 47, 235, 119, 7, 199, 30, 177, 63, 78, 105, 207, 153, 28, 132, 168, 84, 166, 171, 108, 21, 215, 164, 174, 121, 128, 91, 68, 20, 222, 81, 137, 13, 152]

pubkey(q,h):(18172777775303192159727657832771688633216215598877965158949208820296023901084764760222881725262986702478735713462424007788959106272018399708244805316198640706589775789778454299532286932532522325791791312289833643271330941006206604894333175027113622330874626579800679513666624938603337561309816936129926352661091319564303604867093095700819543458178063985869752612663625872468653351930763784372987474747809415652595112648835928004343413910248386752899307068129610089712815257479121368111201632430687614657790581254030567845143865728745079851692195657361359959987504557281840928862881924309178036648485188421874327022341, 392638098592460228418508462226385074690422702429214284385732305774317959159895775092251586043956914155602546821559652111400517952111932579557319610857122515237088379905875982863782386657213421074126519458271560586678974481499715849371311979995450766948182818105567819897007307737370051632369390705725712223883589110699340619034611462216676501782567065261228166297471411589579035544131060706331012337024260046692910523900152236991203944000276133732456285962825434272960749340504092014446362862600803570698206213069473248298100863523331832957430305801141935737006263947843411592717969844892834332104365594346376118846)
c=4605640253217003331334964510174592254013178259349707648547335080743845433538772185582533054930473399495034133342299169373655297635370654237814250924077096784419954824350471683280656146814012837777204413608581553756866045890045788846665715321962704221105416079118007959490372975054302058194463432668018727266982561600329852084442818715440190956213811944269576719501924787366260795121132011879061730892865163591549129768412164655406373350666250339077746317309673325358941772202710386313434421388779073207650619564862431076222163014501544922959835509589742031678624743915535537547452120771609556012990490607104696154771

求解本题关键在于求解mask和msg

先讲讲对msg的求解

求解msg

$\because c \equiv r\times h + msg \mod q$

而$h \equiv f^{-1}\times g \mod q$

$\therefore c \equiv f^{-1}\times g\times r + msg \mod q$

左右两边同乘$f$得

$fc \equiv gr + f\times msg \mod q$

两边再同乘$f^{-1}$得

$c \equiv f^{-1}gr + msg \mod q$

在此基础上，两边再模$g$得到

$c \equiv msg \mod g$，因为$g < q$

所以求解$msg$之前，我们需要先求解$g$和$f$

对$h \equiv f^{-1}\times g\mod q$两边同乘$f$得

$h\times f \equiv g \mod q$

即$g = hf -kq$

构造格

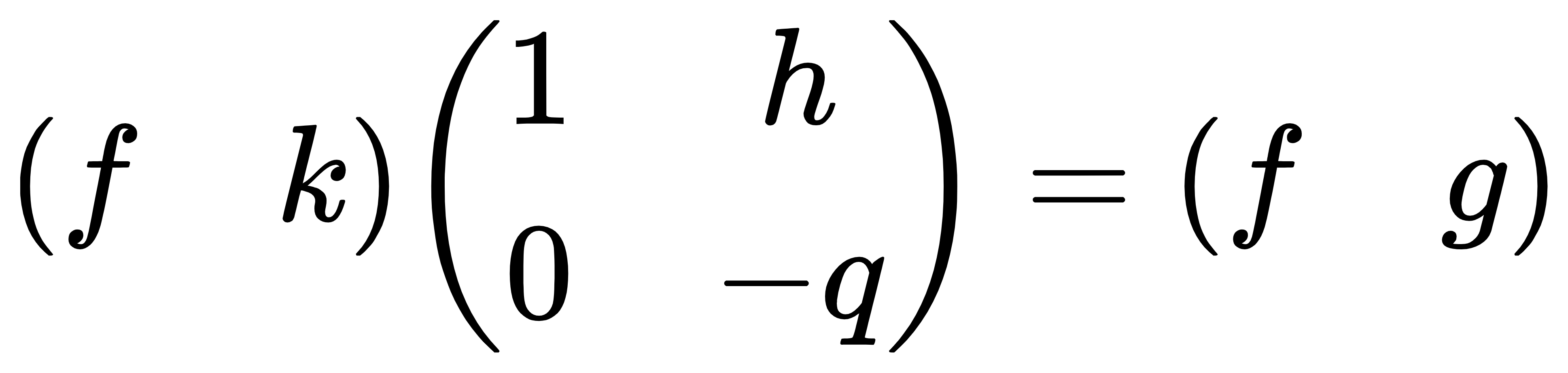
LLL规约后即可得到$f,g$，然后求解$msg$

求解原始P

思路类似于2023BRICS + CTF——sqrt，题目给出256个元素的全排列$P$的平方$P^2$，要求我们通过$P^2$恢复$P$

参考：Crypto趣题-其他 | 糖醋小鸡块的blog (tangcuxiaojikuai.xyz)

首先理解一组排列即是一个置换，而排列的平方就是二重置换，相当于C[i] = P[P[i]]

举个例子

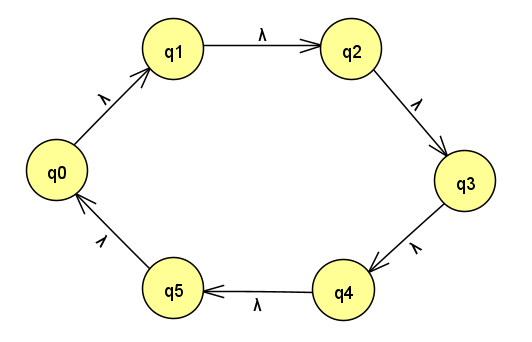
上图为一个置换，表示q0置换到q1，q1置换到q2，…，q5置换到q0

这个置换的平方就是，q0->q1->q2，即该置换平方后q0置换到q2

平方后，该置换变为：

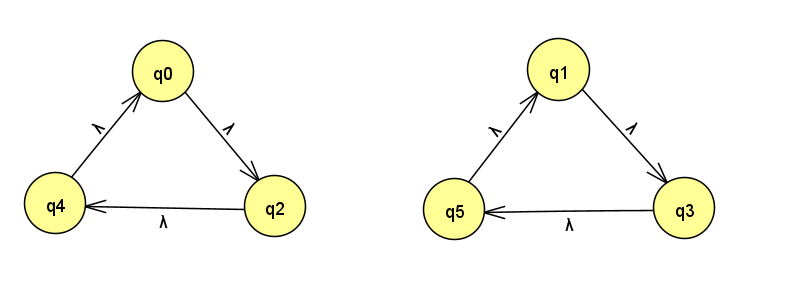
那么还原的方式就是将两个环并排，然后挨个插入，如下：

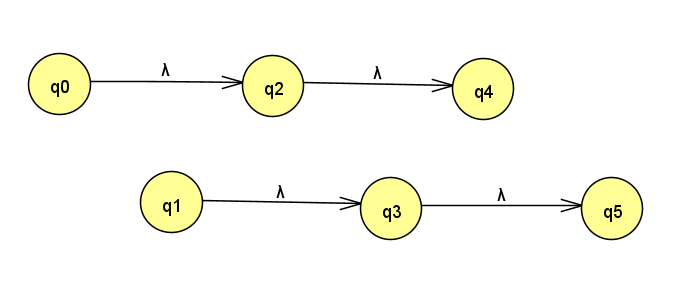
插入后为

如果以这种方式插入的话

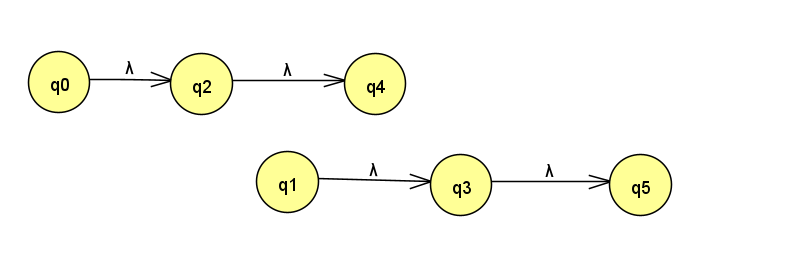
插入后的结果为

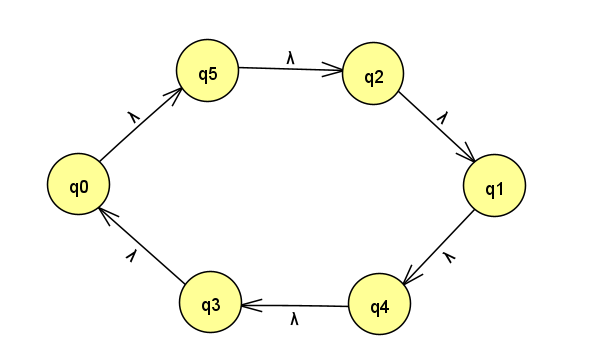
很明显，不同的插入方式，恢复的置换是不一样的，但这两个置换的平方是一样的（这个结论有助于理解后面恢复原始的P）

上述是偶数个元素的置换

下面我们讨论奇数个元素的置换

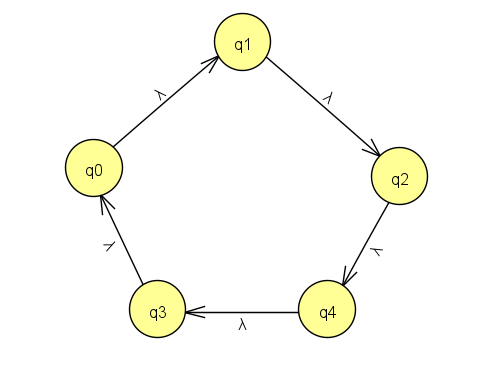
该置换平方后是

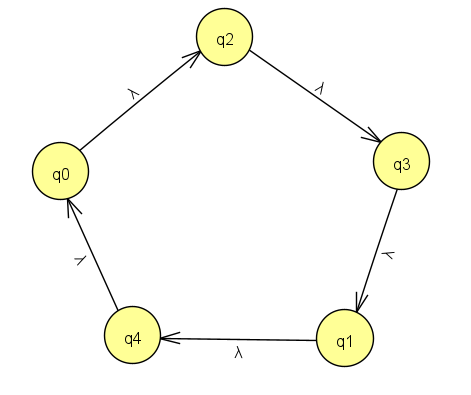
可以发现，奇数个元素的置换平方后，环并没有断裂，只是位置上发生了变化

这种情况下恢复的置换是唯一的

理解上面内容后，即可开始做题

1. 首先要先把平方后的排列切割成若干个环

就如

我们发现q0,q2,q4，q1,q3,q5能构成环

所以我们要在P^2中找出所有环

def find_Chain(P2):
	Chain = []
	for i in range(len(P2)):			#以0~255为环的开头来找环
		head = i
		chain = [head]
		c = P2[head]
		for j in range(len(P2)):		#直到有环出现
			chain.append(c)
			c = P2[c]
			if c == head:				#环出现的标识
				if chain not in Chain:	#环不能重复
					lag = 1
					for k in range(len(Chain)):		#遍历所有环
						for l in chain:				#遍历目前这个环的所有元素，保证它不在其他环中
							if l in Chain[k]:
								lag = 0
								break
					if lag == 1:
						if len(chain) == 2:			#处理单环
							Chain.append(chain[:-1])
							break
						else:
							Chain.append(chain)
							break
	return Chain

Chain = find_Chain(P2)
LEN = []
for line in Chain:
    LEN.append(len(line))

LEN = sorted(LEN)[::-1]
# 2*64 + 2*29 + 2*20 + 2*9 + 2*4 + 1*3 + 1*1

发现找到了2个长度为64的环，2个长度为29的环，2个长度为20的环，2个长度为9的环，2个长度为4的环，1个长度为3的环，1个长度为1的环

2.分析如何还原

对于长为64，20，4的环，它一定是由长128，40，8的环拆分而成

对于2个长为29，9的环，有可能是由58，18的环拆分而成，也有可能是两个独立的长为29，9的环（这种可能的概率很小）

对于长为3和1的环，就是单独的环

本题我把2个长为29，9的环认为是由长为58，18的环拆分而成的

需要注意的是把2个长为64的环拼接成128的环有64种可能，其他也是一样的

首先恢复单环，然后拼接双环，最后恢复出初始置换

也许讲的不是很清楚，建议结合参考文章看，或者与我私下交流讨论

exp:

#sage
from Crypto.Util.number import *
from tqdm import *
import random
import gmpy2
import hashlib

class P:
	def __init__(self, data):
		if type(data) is int:
			self.size = data
			self._list = [i+1 for i in range(self.size)]
			self._initialize()			
		elif type(data) is list:
			self._list = data
			self.size = len(self._list)

	def __mul__(self, other):
		return P(self._iterList(self.getList(),other.getList()))

	def __repr__(self):
		return str(self._list)

	def __len__(self):
		return len(self._list)

	def __pow__(self, other):
		tempList = self._list
		for _ in range(1,other):
			tempList = self._iterList(tempList, tempList)
		return P(tempList)

	def __str__(self):
		return str(self._list)

	def getList(self):
		return self._list

	def _initialize(self):
		for i in range(10):
			random.shuffle(self._list)

	def _iterList(self, List1,List2):
		new_list = []
		for elem in List1:
			new_list.append(List2[elem - 1])
		return new_list

P2 = [82, 237, 32, 83, 30, 200, 116, 114, 4, 147, 171, 152, 193, 19, 170, 136, 186, 8, 124, 159, 225, 6, 180, 125, 74, 14, 255, 60, 187, 132, 222, 121, 56, 79, 57, 229, 87, 27, 72, 197, 201, 191, 75, 38, 135, 177, 165, 149, 17, 172, 173, 59, 210, 108, 31, 142, 163, 227, 178, 226, 73, 256, 190, 12, 103, 238, 129, 157, 219, 131, 67, 28, 68, 236, 168, 209, 245, 93, 61, 122, 208, 137, 49, 94, 111, 18, 161, 106, 54, 175, 70, 16, 110, 5, 218, 81, 233, 45, 91, 188, 151, 104, 148, 184, 228, 248, 150, 176, 167, 35, 130, 242, 126, 156, 42, 169, 232, 102, 50, 214, 179, 205, 9, 235, 97, 84, 246, 36, 76, 240, 52, 144, 98, 86, 99, 21, 64, 217, 15, 202, 206, 55, 244, 65, 23, 53, 250, 78, 22, 215, 25, 66, 143, 107, 195, 80, 196, 254, 174, 33, 162, 252, 141, 153, 43, 185, 211, 220, 115, 127, 216, 251, 139, 95, 146, 48, 239, 241, 37, 199, 13, 160, 90, 223, 123, 181, 120, 164, 118, 112, 128, 192, 249, 39, 2, 207, 71, 182, 145, 62, 3, 92, 183, 194, 100, 24, 133, 10, 117, 234, 29, 11, 140, 166, 85, 224, 230, 134, 189, 63, 46, 58, 231, 247, 47, 154, 44, 77, 89, 101, 69, 40, 26, 243, 253, 41, 51, 105, 155, 138, 1, 212, 20, 203, 213, 198, 158, 88, 109, 34, 119, 221, 113, 96, 204, 7]
mask_hash = "91881f508f08fbafec1a6879fc3a1f215135c94c78f03fae8534d54dc05bd4a122a4e4508d32b9e02be08fbbb42a9e3335fc433c20e2da2e012d11b7324f6952"
mul = [114, 189, 92, 56, 252, 161, 202, 250, 131, 9, 111, 226, 223, 24, 14, 6, 99, 208, 195, 216, 141, 116, 167, 34, 5, 129, 15, 158, 178, 197, 4, 187, 27, 200, 144, 76, 74, 154, 86, 249, 93, 112, 46, 104, 25, 248, 40, 225, 38, 98, 186, 169, 64, 118, 33, 88, 26, 106, 183, 43, 201, 198, 242, 135, 110, 218, 244, 120, 83, 212, 192, 185, 148, 142, 11, 45, 232, 107, 18, 170, 60, 130, 247, 67, 65, 211, 182, 213, 134, 254, 70, 191, 210, 176, 145, 217, 82, 229, 125, 193, 155, 41, 113, 103, 49, 231, 133, 75, 109, 238, 126, 245, 163, 233, 227, 181, 51, 12, 143, 234, 239, 59, 240, 209, 42, 205, 230, 253, 203, 219, 23, 136, 32, 87, 102, 94, 85, 62, 172, 236, 124, 100, 256, 196, 50, 101, 206, 150, 89, 29, 61, 69, 246, 237, 16, 37, 184, 90, 162, 22, 36, 10, 31, 52, 190, 17, 55, 115, 251, 77, 214, 122, 1, 255, 151, 157, 241, 224, 3, 44, 48, 175, 194, 138, 179, 159, 160, 53, 80, 73, 8, 35, 156, 117, 58, 140, 221, 180, 72, 123, 147, 95, 228, 97, 71, 204, 39, 149, 2, 19, 173, 139, 146, 54, 96, 220, 79, 66, 57, 127, 243, 188, 165, 47, 235, 119, 7, 199, 30, 177, 63, 78, 105, 207, 153, 28, 132, 168, 84, 166, 171, 108, 21, 215, 164, 174, 121, 128, 91, 68, 20, 222, 81, 137, 13, 152]
mul = P(mul)
q = 18172777775303192159727657832771688633216215598877965158949208820296023901084764760222881725262986702478735713462424007788959106272018399708244805316198640706589775789778454299532286932532522325791791312289833643271330941006206604894333175027113622330874626579800679513666624938603337561309816936129926352661091319564303604867093095700819543458178063985869752612663625872468653351930763784372987474747809415652595112648835928004343413910248386752899307068129610089712815257479121368111201632430687614657790581254030567845143865728745079851692195657361359959987504557281840928862881924309178036648485188421874327022341
h = 392638098592460228418508462226385074690422702429214284385732305774317959159895775092251586043956914155602546821559652111400517952111932579557319610857122515237088379905875982863782386657213421074126519458271560586678974481499715849371311979995450766948182818105567819897007307737370051632369390705725712223883589110699340619034611462216676501782567065261228166297471411589579035544131060706331012337024260046692910523900152236991203944000276133732456285962825434272960749340504092014446362862600803570698206213069473248298100863523331832957430305801141935737006263947843411592717969844892834332104365594346376118846
c = 4605640253217003331334964510174592254013178259349707648547335080743845433538772185582533054930473399495034133342299169373655297635370654237814250924077096784419954824350471683280656146814012837777204413608581553756866045890045788846665715321962704221105416079118007959490372975054302058194463432668018727266982561600329852084442818715440190956213811944269576719501924787366260795121132011879061730892865163591549129768412164655406373350666250339077746317309673325358941772202710386313434421388779073207650619564862431076222163014501544922959835509589742031678624743915535537547452120771609556012990490607104696154771

Ge = Matrix(ZZ,[[1,h],[0,q]])
#print(Ge.LLL())
f,g = Ge.LLL()[0]
f,g = abs(f),abs(g)

def get_msg(c):
    temp = f*c % q
    m = gmpy2.invert(f,g)*temp % g
    return m

msg = get_msg(c)

for i in range(len(P2)):		# 防止P2[256]导致溢出
    P2[i] -= 1

def find_Chain(P2):
	Chain = []
	for i in range(len(P2)):			#以0~255为环的开头来找环
		head = i
		chain = [head]
		c = P2[head]
		for j in range(len(P2)):		#直到有环出现
			chain.append(c)
			c = P2[c]
			if c == head:				#环出现的标识
				if chain not in Chain:	#环不能重复
					lag = 1
					for k in range(len(Chain)):		#遍历所有环
						for l in chain:				#遍历目前这个环的所有元素，保证它不在其他环中
							if l in Chain[k]:
								lag = 0
								break
					if lag == 1:
						if len(chain) == 2:			#处理单环
							Chain.append(chain[:-1])
							break
						else:
							Chain.append(chain)
							break
	return Chain

Chain = find_Chain(P2)
LEN = []
for line in Chain:
    LEN.append(len(line))

LEN = sorted(LEN)[::-1]
# 2*64 + 2*29 + 2*20 + 2*9 + 2*4 + 1*3 + 1*1

chain64_1 = [0, 81, 136, 63, 11, 151, 65, 237, 104, 227, 76, 244, 212, 139, 201, 91, 15, 135, 20, 224, 46, 164, 42, 74, 167, 219, 62, 189, 111, 241, 211, 10, 170, 215, 223, 246, 157, 253, 95, 80, 207, 9, 146, 249, 33, 78, 60, 72, 67, 156, 195, 206, 132, 97, 44, 134, 98, 90, 69, 130, 51, 58, 177, 240]
chain64_2 = [1, 236, 50, 172, 138, 14, 169, 126, 245, 197, 181, 159, 32, 55, 141, 54, 30, 221, 57, 226, 43, 37, 26, 254, 203, 193, 38, 71, 27, 59, 225, 153, 106, 149, 214, 84, 110, 129, 239, 137, 216, 229, 100, 150, 24, 73, 235, 40, 200, 2, 31, 120, 178, 36, 86, 160, 161, 251, 220, 45, 176, 238, 154, 194]
chain29_1 = [4, 29, 131, 143, 64, 102, 147, 77, 92, 109, 34, 56, 162, 140, 205, 23, 124, 96, 232, 25, 13, 18, 123, 234, 252, 112, 125, 83, 93]
chain29_2 = [7, 113, 155, 79, 121, 204, 99, 187, 163, 152, 142, 243, 202, 182, 89, 174, 145, 52, 209, 233, 242, 19, 158, 173, 94, 217, 133, 85, 17]
chain20_1 = [3, 82, 48, 16, 185, 180, 12, 192, 248, 108, 166, 210, 28, 186, 119, 213, 165, 184, 122, 8]
chain20_2 = [5, 199, 61, 255, 6, 115, 168, 114, 41, 190, 127, 35, 228, 88, 53, 107, 175, 47, 148, 21]
chain9_1 = [39, 196, 70, 66, 128, 75, 208, 116, 231]
chain9_2 = [68, 218, 188, 117, 101, 103, 183, 222, 230]
chain4_1 = [22, 179, 198, 144]
chain4_2 = [49, 171, 250, 118]
chain3 = [87, 105, 247]
chain1 = [191]

dictionary = {}
def deal_SingleRing(chain):
    new_ring = [0 for i in range(len(chain))]
    for i in range(len(chain)):
        new_ring[2*i % len(new_ring)] = chain[i]
    
    for i in range(len(new_ring)):
        dictionary[new_ring[i]] = new_ring[(i+1)%len(new_ring)]
    
deal_SingleRing(chain1)
deal_SingleRing(chain3)

for i1 in trange(64):									#处理2*64的环
    ring_128 = [0 for i in range(128)]
    for j in range(128):
        if(j%2 == 0):
            ring_128[j] = chain64_1[j//2]
        else:
            ring_128[j] = chain64_2[(j//2+i1)%64]
    for j in range(128):
        dictionary[ring_128[j]] = ring_128[(j+1)%128]	#添入字典
        
    for i2 in range(29):								#处理2*29的环
        ring_58 = [0 for i in range(58)]
        for j in range(58):
            if(j%2==0):
                ring_58[j] = chain29_1[j//2]
            else:
                ring_58[j] = chain29_2[(j//2+i2)%29]
        for j in range(58):
            dictionary[ring_58[j]] = ring_58[(j+1)%58]	#添入字典

        for i3 in range(20):							#处理2*20的环
            ring_40 = [0 for i in range(40)]
            for j in range(40):
                if(j%2 == 0):
                    ring_40[j] = chain20_1[j//2]
                else:
                    ring_40[j] = chain20_2[(j//2+i3)%20]
            for j in range(40):
                dictionary[ring_40[j]] = ring_40[(j+1)%40]	#添入字典
                
            for i4 in range(9):								#处理2*9的环
                ring_18 = [0 for i in range(18)]
                for j in range(18):
                    if(j%2 == 0):
                        ring_18[j] = chain9_1[j//2]
                    else:
                        ring_18[j] = chain9_2[(j//2 + i4)%9]
                for j in range(18):
                    dictionary[ring_18[j]] = ring_18[(j+1)%18]	#添入字典
                    		
                for i5 in range(4):								#处理2*4的字典
                    ring_8 = [0 for i in range(8)]
                    for j in range(8):
                        if(j%2 == 0):
                            ring_8[j] = chain4_1[j//2]
                        else:
                            ring_8[j] = chain4_2[(j//2+i5)%4]
                    for j in range(8):
                        dictionary[ring_8[j]] = ring_8[(j+1)%8]
                        
                    M = [dictionary[j]+1 for j in range(256)]
                    mask = P(M)
                    h = hashlib.sha512(str(mask).encode()).hexdigest()
                    if h == mask_hash:
                        print("P =",mask)
                        
                        temp = hashlib.sha512(str(mask * mul).encode()).hexdigest()
                        flag = long_to_bytes(msg^^ int(temp,16))
                        print("flag:",flag)
                        break
                        #ISCTF{You_can_very_good_at_permutation_and_lattice_base}

Misc

Beyond Hex, Meet Heptadecimal

题目描述：

我：给我来个自创的古典密码编码类型的题目
chatGPT:明白了，你想要一个编码题目，但它应该有一些非传统的编码方式。让我给你设计一个类似的题目。
你获得了一段看起来像是十六进制的字符串，但解码后得到的内容并不是预期的文本。你需要深入挖掘，并发现隐藏在其背后的秘密！

密文：

ID71QI6UV7NRV5ULVJDJ1PTVJDVINVBQUNT

根据题目意思，不止是16进制，猜测A对应10，B对应11，以此类推

然后把密文中的字符转成对应的数字

然后发现这些数字最大是31 = 2**5 - 1，猜测有可能是要把数字转成长度为5的二进制串，然后拼接

最后长度为7进行分割，因为这样刚好能表示0~127的值，就是ASCII码的范围，再转回字符

exp:

#先生成字典
table = {}
for i in range(10):
    table.update({chr(48+i):i})
for i in range(26):
    table.update({chr(65+i):10 + int(i)})
    
cipher = "ID71QI6UV7NRV5ULVJDJ1PTVJDVINVBQUNT"
#找字符对应的值
position = []
for i in cipher:
    position.append(table[i])
#拼接成二进制串    
binary_str = ''.join(format(i, '05b') for i in position)
#分割
grouped_binary = [binary_str[i:i+7] for i in range(0, len(binary_str), 7)]


flag = ""
for i in grouped_binary:
    flag += chr(int(i,2))
print(flag)
# ISCTF{so_ez_flag_for_uuu}

你说爱我？尊嘟假嘟

密文：

你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 假嘟 尊嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 假嘟 你说爱我 假嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 尊嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 你说爱我 尊嘟 尊嘟 尊嘟
尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 你说爱我
假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 尊嘟 假嘟 尊嘟 尊嘟 你说爱我 假嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟
尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 假嘟 你说爱我 假嘟 尊嘟 你说爱我 假嘟 尊嘟 你说爱我 假嘟
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
尊嘟 假嘟 尊嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 假嘟 你说爱我 假嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 你说爱我 假嘟
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
尊嘟 假嘟 尊嘟 尊嘟 你说爱我 假嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟
尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 假嘟 你说爱我 假嘟 尊嘟 你说爱我 假嘟 尊嘟 尊嘟 尊嘟 尊嘟
尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 假嘟
尊嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 假嘟 你说爱我 假嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 假嘟
尊嘟 尊嘟 你说爱我 假嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 假嘟 你说爱我 假嘟
尊嘟 你说爱我 假嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟
尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟
假嘟 尊嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 假嘟 你说爱我 假嘟 尊嘟
你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 尊嘟 假嘟 尊嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 假嘟
你说爱我 假嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 你说爱我
假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟
假嘟 尊嘟 尊嘟 你说爱我 假嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟
尊嘟 尊嘟 假嘟 你说爱我 假嘟 尊嘟 你说爱我 假嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟
你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 假嘟 尊嘟 尊嘟
你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 假嘟 你说爱我 假嘟 尊嘟 你说爱我
假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 假嘟 尊嘟 尊嘟 你说爱我 假嘟 尊嘟 尊嘟 尊嘟
尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 假嘟 你说爱我 假嘟 尊嘟 你说爱我 假嘟 尊嘟 尊嘟
尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 你说爱我 假嘟
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
尊嘟 假嘟 尊嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 假嘟 你说爱我 假嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 尊嘟 假嘟 尊嘟 尊嘟 你说爱我 假嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟
尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 假嘟 你说爱我 假嘟 尊嘟 你说爱我 假嘟 尊嘟 尊嘟 尊嘟
尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟
尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 尊嘟 假嘟 尊嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 假嘟 你说爱我 假嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 假嘟 尊嘟 尊嘟 你说爱我 假嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟
尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 假嘟 你说爱我 假嘟 尊嘟 你说爱我 假嘟 尊嘟 尊嘟 尊嘟 尊嘟
尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟
尊嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 假嘟 尊嘟 尊嘟
你说爱我 假嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 假嘟 你说爱我 假嘟 尊嘟 你说爱我 假嘟 尊嘟
尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 你说爱我 假嘟 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 假嘟 尊嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 假嘟 你说爱我 假嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 尊嘟 假嘟 尊嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 假嘟 你说爱我 假嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 你说爱我
假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 尊嘟 假嘟 尊嘟 尊嘟 你说爱我 假嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟
尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 假嘟 你说爱我 假嘟 尊嘟 你说爱我 假嘟 尊嘟 尊嘟 尊嘟
尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟
尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 尊嘟 假嘟 尊嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 假嘟 你说爱我 假嘟 尊嘟 你说爱我 假嘟 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 假嘟 尊嘟 尊嘟 你说爱我 假嘟 尊嘟 尊嘟
尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 假嘟 你说爱我 假嘟 尊嘟 你说爱我
假嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 你说爱我 假嘟 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 假嘟 尊嘟 尊嘟 你说爱我
假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 假嘟 你说爱我 假嘟 尊嘟
你说爱我 假嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟
假嘟 尊嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 假嘟 你说爱我
假嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
尊嘟 假嘟 尊嘟 尊嘟 你说爱我 假嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 假嘟
你说爱我 假嘟 尊嘟 你说爱我 假嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟
尊嘟 尊嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟
假嘟 尊嘟 尊嘟 你说爱我 假嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 假嘟 你说爱我
假嘟 尊嘟 你说爱我 假嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 假嘟 尊嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 假嘟 你说爱我 假嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟
你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 假嘟 尊嘟 尊嘟
你说爱我 假嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 假嘟 你说爱我 假嘟 尊嘟 你说爱我
假嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
尊嘟 假嘟 尊嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 假嘟 你说爱我 假嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 假嘟 尊嘟 尊嘟 你说爱我 假嘟 尊嘟 尊嘟 尊嘟 尊嘟
尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 假嘟 你说爱我 假嘟 尊嘟 你说爱我 假嘟 尊嘟
尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 假嘟 尊嘟 尊嘟 你说爱我 假嘟 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 假嘟 你说爱我 假嘟 尊嘟 你说爱我 假嘟
尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟
假嘟 尊嘟 尊嘟 你说爱我 假嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟
假嘟 你说爱我 假嘟 尊嘟 你说爱我 假嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟
尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 你说爱我 假嘟 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 假嘟 尊嘟 尊嘟 你说爱我 假嘟 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 假嘟 你说爱我 假嘟 尊嘟 你说爱我 假嘟 尊嘟 你说爱我
假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 假嘟 尊嘟
尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 假嘟 你说爱我
假嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟
你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 假嘟
尊嘟 尊嘟 你说爱我 假嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 假嘟
你说爱我 假嘟 尊嘟 你说爱我 假嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟
尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟 假嘟 尊嘟 尊嘟 你说爱我 假嘟
尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 假嘟 你说爱我 假嘟 尊嘟 你说爱我
假嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 尊嘟 你说爱我
假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 尊嘟
假嘟 尊嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 假嘟 你说爱我 假嘟 尊嘟 你说爱我 假嘟 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我 你说爱我
你说爱我 你说爱我 你说爱我 尊嘟 你说爱我 假嘟 你说爱我

三种不同信息，尝试Ook

你说爱我->Ook.，尊嘟->Ook!，假嘟->Ook?

Ook解密得到ild3l4pXejwPcCwJsPAOq7sJczdRdTsJcCEUsP1Z

base64解密：ISCTF{9832h-s92hw-23u7w-2j8s0}

张万森，下雪了

用题目给的字典爆破压缩密码为blueSHARK666

得到tip.txt，发现是非常长的数据

尝试多次base64解码，解了17次后发现无法进行

最后得到的信息为

CIcTpGI3CjMSCTYFdoCTNIIXpIbXZ0ISCadICZI39IbSJYII2CMISxSnSjIE5YFmxaeISXNICSZTp0SmpIYSCXFXdIMGZTSmxacSCICIdTbIpSSmpCYSTXCXTFaFxqFm2IcISCNFNSSmZySmxaC2CIbDZIZCSTSDIadGIGFTdSZF0ESCIaYIZ0S30jZ2ZOY3CIIICGITdSMSS5FF5OSGJGImIIa2C2S3CZeIdICGpSZnB5I3S3b2FyI3djZIpXYICZeITFZmIjMF52SG2IF2YCaG9IbX00CDAIeGJSIT00M2JxIS0IS2dIbICXbXZSYTSIMITSa0NXZTpCSF53SmJFZT0IMIpXYFxac2dCbINNSXACSmxjeE20FX0FbGZYSTdoISTIaINIMSJXSm5OC2JIcETFbIF2YFCacmJESmIISnBFSmxaYF5IInSXbGZpFm5CeSCqQmCIMF5GC2CoaSJFSm9FSm0DFFxadGNIcE5IbIY2SIxob2C0InNCbGZaYT0IM2CCeGIjSTJTC2CIFFJZITpXbIC0CDJ3Z2dYaIZ0Mn0XIIxobFZIITSZIG0FSmCaeTTSImC0ZTS5CEZIS2YCQ30IMjIXSjIIdSZCbINSZnBaSTdIIFSyIX0XbTJOS3C3cTZSF3NOZTpTCTCOaSJZbDCISCSTSm23Z2NFcIdNZnByICJ4YSCIInZ0Z35XFTSINTCIF3CNZ2I4S203CTCCaIdCS2MxSTCIcTCFCIZNIEJXSjSxMIdGIXdXaF0aSTdIeTTII3CXS3CCY3C3aSCISjNIbXB0SG2IZFNIImIIMn0FIIx3bFSIIT0jZF5aSm24IIYyNSNFMSpICTCISmJYa0pFbIpyCI2OZ2p0aINNIEJYS2ZCYIExC0JNSIZYYmxIIITIaE9OZmC4SFCTa2CCFnpCMIpZYSCOZTNIITdSZT4TSGCaFmSIFTTSZTCoCIx3b2CXcECOZTp0SIx3SFJZNSBCa2p2CFCIZTdZOSdISECXSGxIQ2YyITT0IEpXYCJICI3yMF9CZTC0SF2IS2JIb2TIMSJDISdNeIdICIZSbIpoSITxFFNGSnIIa2ZYSm2IIICCMDS0ZCIXY3ZOSSCCaExIZ200FjIOcFIGSTdNMEpCSm2TYIMxITdCb3pQSmx3SITZInCTZTpyI3ZIaE2ZIT0IMnZ0SjI3IISIbIp0MXACISSac2CICnJPS2BOSjIJeICIY20NZTS5FFx3SGJIcITCaFZICDI3S2CFZTdNIEJSSm24IFIIIX0CbmxXFmxIaIpEITdjMIZCY3dIFT2GcITIZmQICDJISFECCI0SSGxCIICacT5IIT0NSCTYFmxIeT3IF39IMDISSIxoSmJYaDNSMGZPFTd3Z2pGCGT0M0BMSmTIeGQxCnZIa2pPSTdoSITFZndFMSpTCSZIS32Xe0TIbCSZSTC3c2NIaI00M3TxS3dCeIYxC0S0ZTpOYmx3b2dXdGICST24I30IaTJCaG9FSm0DYjI3S2dCdIZNSXAIS3dTa2YyI300Zm0SS3SaCIYIImIIMIZTFmxISFEydCIISEoIYCICeSNZCI0SSGxISmxaI2dGITCXbFCCCSdIMISCMCBFbFp0YTCISFIZInCCe3CCYCI3cFIGImTIZ20YS2dTYSMxC3dXIGZYYTSacTSqQCIIMSI4SF2TST2ZcEpSS2B0SjJGcmECaICTa2p0ITCaIFZICnZjZ35YFjJob2CZImpNSTJTSmC3IId0FT0Ia2p0STCIS2pGCmxIbEp6SjJCNIIGInJjI0BaS3F2cTCqI3CIS3pxSGxaS2JIcDCIa3J0SCI3IINZCIdSZF0FSIcxb2TIIX0CMF0IYXpGISC0eGCIM3pyCTC3ImEyFTZCMSpXCEdIIIJCeINSIEJ3S3CIF2YxITCNSmZqFT0CYSTFZ3CXZmZXSFCTIIJIIn0IZ20ZSCI3SFN0OS0XIEJMSXpGI2YxSnSFbGZpFjI3d2CCcECSMSJCS20oIGJYFTBSbXN4C3C3cTCCOSCNa2Y2ISSaF2dCZX0jZF0XCFCIaIpISCIIbIJCSmx3aSNIICJIbCB2CFCJeIpSCT0XZ2JQSmTxb2Yxb0N0ZCTIY3d4S2YydDB0bFYFSmx3SF2IcDNIMIpPFmxOcFJGCIdISC02S2CIZ2dCS3daIICIY3F2cIYII3CSZmZXSII5F32SNXpIMn0SY3C3NmJSQTSIM2JoITd4YSN0F30PSFxCYCNBd2dISmISMIZCSFCaIGJXaG0Ia35SS3CZeIS0dGCIa2B6SFCaaFIIM0dCSECXYCI3IIdIITCTZTpCY3CIaE2YQn0IS2Z0ISC3ZFJGaGCCZ2JQIICaIFSIIXTTIGZoCFZGZTSCe0dIMSoFFm5aSFExcIBSbX0PYCJOZ2p0bI0ISXBISm24F2MxIX0CIGxSYCIIIITZSCIjZTCCSIx3S2CIcE0IMjEISmIxZSJIaIdSSICFIICaIFNZNS0PSTpoYCBIISCGF3djbSI4I30ISIJ0F39IbG0DCmx3SSICdGTNS20YSCJTYIIIInZ0Zm0aSjNIaIYIInNObEp2I3COCmExcEpXS2Z0YjISeSJYcIJSSSpYIIxoFFIGCIdaZSpIFmxIITTSITd0S3T4FF53S2C6ZCBaZECZSjJ3ISNCZTN0eTCaSmTIeE50SnNXbTJIFjNISTZIIndTbGC2SF5OITCIcI0CMIpDSjAxIISZaISSIG0MIXp3Z2SyC3COS35pYCBINSCCcEdCSmxXSI0oIId0aITCbXZ0SjIIcTpGCmpIbIoISGxIC2dGInZSb0BaCFCCd2CFQX0IbFpISIx3SFSIITSXSTp0FCJIIIJZCICSZTpYITdTYF2ICI0jZIZaSjI3ISC0dGI0MFpSSmxIImEyFXpFSTp0STC3dE9XbE50MXBCSTZJMSFyZ3dCb35FY3doSTCICINIZTpySF2GF2CZcDBSbCEISCIaZTdIcIdIZSpyI3ZGFFMxC0SFbIxOCIx3ITdXdGICS2JCY3CIFFJSQnJFSSJ0STC3cTdICm0IaFIFISSaa2dGIXpSb3pXFjNONICqZmC3STJCYFdoC32ScDSIbGZ2FjIIS2ZFCmTCZXBCIIxoF2CIb0NIbmZIY3CaMI3ISCSXZ3pCYTZCS2YCQm0XSTp0STCIc2IIcE5SaCETSm2IZFEyF30IaFZSYTd4b2ZSaENSbIpTCFdIaT2EZT0SbCSCSjJ3c35IbIpSIG0MICIaSFMxcEdFbG0XYT0oNTCqIX0IMSp0FF5OaTJXeICCa2paCDIISTdCZmpSSCSGSSd4a2YySnNXa2CXYTZCNIS6ZmCIMSp2FmxIaSJFQTBIbCAxFCJJeIpGSTNSSSpISIC3F2dISnZ3Z2ZaSmCISTCCeG9ISTpCSFpOS32FaG0Ce3CXYF2OZ35ICG0Ta2S4SmxjeE50ZX0XaF0FYmI2SSTIFnNIMSJISF2GSSJIc00SbCSPSTCJeINZbICSIG0YSTZ3I2N0FjCZbGZoYCJ2MICGSmCIM35yCSC3aSJZcG9FSm0DSTCadGNIOITNSnBSIICaYSTIInZSb3CaYCJISIpIInNjbGZTCEdoFT2GICIXa2CCSCICeSJYaIZ0Mm0CSmTxF2CGSnIIaCTqCICIISTZI390S35GFFpOSFJFZXdCSEExFjI3IIIGaGTSZXBQSm2TYSMyCnNSbG0IFjBac2TZIndXSTJCSmpCIIJZbDNCMIp2SjIaNTCZaIdNa3CMSIpGaFZ0Z3dXaCSCYmC3NSYxF3COZTS5SIC3SGJZNS0CbGQTSTCadGSSImxIb0B6SjSxMIZIIXdNSIJXCSdoeTCFI3CjbF5SC2CIS2JYQjJIbXB0ISdOc2dFFTNSIEJYII2TI2dIInICa3JOFm2IIIYxaGC0bEpYYFCoSSC6SnCCMn00STC3dIJIaId0MI94Smp3NGEyZTdXa2pFS3S3IISqCTNjbIpYCSC3ST2IIjIIbX0XYSCJeIIGcIdIMTJSSXp3ImSGC0N0ZCSYFTS3FICCMCZ3MIZ0SF5IC2CXFTdFS2ZXCmxaIGSGCTdIb0B6ICBIb2CXZX0jZTC0Sm2IFIZCeGIjMXB0I3F2SIJScECIa3CCFCISeINYaI0SaCSCSjBoQ2YxbI0je3CYFm24ISpIaGCIS3pCYT0IST2FFXdIa3C0YFx3dINGcE5IMFoyS2CISmQyFX0Fb35CY3dIC2TCMI9SMST4SF2GSIJII30CMICZYFC3c35XOSSIMF0MSjBaa2d0F303ZFxOSm5CISCCMDIFMST5FF5ISmJ0eI0CbG0SCIxIcTdCdGpSZTp5S3cxb2FxI3CXbGxXYTZGM2CFZTp3MDICFmx3aSJScITIZTCZSCIIZFECbGpTa2pYSIdTd2NGa2dXbXZICSCIIIYyeGIIM3pSFTZCIICIcGIaSTpXYFx3c39ICGTCZFpYSjI3MGEyIX0XaFZpFTSIaISZSCIFMSpTCSCObGJGcDBaSIZ0STFxSFJECTdNbTJ6SmTxI2dIZnZ0ZmZXFT0CCSCFQmCIMF50FF5OSFJ0FT0CbXZTSGxac2pEQTpIMIYTSjIob2TIC3CjIEpIYTZGSICEZnNXST50I3CICTCFQTdISEp2SCJGZ32ICId0aCSISmx3bFSIbICXa2ZXSmCIeTTSImC0STpyFFCoS2JIIm0Ce3C0SjIIdSNIQTdSS3pQSmTIMSICS3dXb3paCCJoSIZIITdOSTS5CFdTS2SIcDISS20CSjJ3IIIIeICNZnB0ITCSeIYxcE0jZCSXCSSIaIYxITd0MFT4SFC3SId0aISCa2p0STCIdGSSCGpSZnBISSCob2FIMS0Sa3CXSnpId2CFQXdTZ35TYFC3aSCIICJIZTp0FF2IIIJYcGIIbI0IIS0IS2dICI0TZmZZCSF2IITZImIIM3pGCTCoSSYCFT0Fa2pyCDIIZTpGcId0MTJSSmp3d2QxInJNSIZXS3SaIITXd0dCZTCxFm53SISIcE0XaFZSSGIxZmN0OSdSSESTI3ZGCmQIMSCaZmZYFjJoSSCqQmCSM3C0ST03S2CIITTIbCETCFCZemNICI0Ib0AIITSaYSCZMXIZSECXCI5oaIpICIdIMIZCSF2IIIJZIXpIMSpXISCNeSZYbIS0MTJCIICad2Qxb0ZTZIZOCSCIeISXMFdXbIT2CSZIIGEyaE0ISEpTFjJOISIICE5IMFoySmpGYSTXF30Fa2pZFmx3C2CqZ3CCbIpYCSZCITCIbDSSMnZSSm23IGIGCIp0MXBoSIZGcFNIInZ3ZmZOSmxINSdZSmIIMSJTFmpaF2CIIT0FSCSCCGxaZSJIcGxIaCS5SjJCNSdGITCjZm0YSjNodTTqQXdTZT5GSmxOaSCIcIpIS2B0ISCOS2SYaI00M2JIIICacT5IbICXb35XCICaeSTFcENXbIpGSF5ISFIZITBCMn0ZYCIIdGI0eGTXZF0aSmpGaT50IXTCIGxXYmI2S2TCcCIXSmxySF53a32Ic00SbCI0S3d3ZFNIbISIbFTxSm2CeGNICISCbGZpSTC3NTCqQmICS3pCSG5ISGJSQm9CSEC2YjI3cTCCZTZNS2JCSI2TaFIGIXTTZm0SSnpGdTYxITpTS2CSCEF2FFJYaI0IZTCSYjI3IINFCTZSaCSXISdCMSCGa20XbE5XCICaZ2C0eINSM3pCYFCoSFIZbDZFSSp0STCOcTdCcINISnBYSm2IC2FIM00Xb3CFYCNIISCqQmICbIS5CFC3aIJFZnpSMnQTSTd3Z2dCaI0Ib0BySmp3C2JIC0JPSmZpSjJoSTYxITNFMFS2CS0OIGJZNSdCSEExISCacSJZCE9IbSJ5SmTxMGIGInJOSIZaCFCIeTYyeGIIaCSXSIx3aE2YQTTXa2CZSjIOSFNII39IaCSISjB3CT5IInZ3Z2BZCFZIIIdZSmCIZTpyYT0GS320FCBIbX0CYFx3dSpINF5IbXcxSFxIa2SxIXdNIEpPST0CS2ZXNI9NMSpxFFCTST2SNXTCSSpSYSC3cFNSbId0MFpSSCSxS2NGFnJXbFCCCI2oSSdXeGICMTI4SFxobIJ6bINFSTC2STCCeF5SdI0IM0BXSjSINSCIInNjZI0SYCIIYSpSCEdCZCTXI3F2aETIICIIaFQTYCJJeIdFFTNSa2BSIIx3b2dGbISIbmZYFm5CZ2dZI39IZTp2FICoITCIc0JCSTp0YF2OIIJICE5SbEpCS2CIZ2NCS3djZIxSY3docISCe0dISmZXSICTaF2XF30IMjSXYIx3dISICICSSECFSjBaImSXF3SZbIpOYCNCIIC0eG93MIZTFT0oaTSyaGIIbX02YFxIcSJZOS0IMDSSISS3c2FIMSCIa35XCSC3I2pSITd3ZTpCI3CIaIECQndIS2BDISCaZFJSCmIIemxyIIC3FFSIC0JSaT5YY3CIeSZIIm9IMDIxSmCoSFExcG0SbX0ZCEC3c2p0bI0IMmcySmC3NITIIXTSa2pPSmxIcTSCe0dFMIxSFm53CFJGcICSMI0SSCAxSFNGaIdNaTCQISd4I2JZNSd0ZTppFm5BeTdIImI3MST4SFxIaIJCFnBSMICTF2CacTpScE5IMIpJSmT2C2d0ZXpZbG0aSjNIMTpEZmCIMIZCFF24FFJIImIXSTC0YjJGIINZImpCZ20YSmpOF2YxFTdXbXZCCICIITC0eGI0ZCIISmxCS2JIc0CSSECaCFCIISNIaGTXZ3pFS2d4S2dZMXNIbTJIFnpIISSqQTdOZmC2YFdGIGJGcDBIS2QTSm23SSJIQTC0a2poIXp3Z2SxcE0SZ35YFTSIFICCM00OZTS4SI0oSId0aISIMGZSS2CIdGS0ZTdSZ205SjS2aFIIInNXbm0IYT0Zd2YICECIM350Y3CISFJIcISIbXZICFC3Z2CFCm0IbSJYSIZ3bFSIInICIG0XCII2eTdZaE9XZTpJFI5CSmJYaDJaS200STCGdIJCcE50eTYFSmTIMSQxIT0CaF0IYXpIS2TFZmICSnBISF2TST2IcDBSbX0TSGxadGZ6QTd0aF92S2CaSmSIInSFbIJpFjJoaICCcE9SM3C0SFCaIGJZc0NSbCICCIx3cTpSCISSZ2J0SCJTc2YyZXTSaTpSSmxISIT6ZmCjM3p0FFx3F2CFQTpIMIQTSCIIdT5SCGpISTpFIS0ISFMxSnZTZXZYY3d4eSYyeGC0ZTT2SmpaSTYCaE0Ia3pTSTCGcSSIcG00MXBCSm2IZFEyFTdIbTJIFmx3SIZISndOZTpCICNoC2SIMCNFSI0SISCOZmN0ZmIIMF0oIIpGYIMxSnJaZm0CYT0ZeTdISmpOSTT5FFC3aISZcIdCbG0CCGxacSNZdI0IbEp4STd4aFI0ZXpZbECXSjNCCISqZ3pTZnBJFFI5ST2Ca0dISCAxFCIZeIdFZTNSSSpSSISIS2NGI30OS35XCICIeTFyeINXbIpGYnpCS2CIInpCMn0ZCICIIGNGCmTCZF3xSm2IImSGIX0IIG0FYmx3S2TCMCZXZTpxSGxOamJGbDSaSIZ0YI23SmNIITdIMF0FISSSeGZ0Z3dIbGZpSTdoeSCYcEdCbSCXSI53IGJIIT0CbIpTCDIadGZGCIdNZIC6SFCoC2TII3dCbFCXYT0IeTZZImCjbFC0SGxaCmECQTpXbICICTCCeSNISTd0MDSoSICIYIIGIXdaZmZFFTZIIS3ISCI0ZCB2FFCISFJGI3CFSTpICSC3cTpGFmTSZXBYS2d4S2TICEdSZm0qCICaSTZIaENIMST5CSS3aGJScETIS2B0SjIJemISITpIb0BTITSaC2dIcEdaZmZIYCIIM2YxITNCMFT4S20oSIJ0eG9SbX0TS2CIcSJZdI0Ib0AISGxoa2SZMFSIaF0XSjNoaIYICECIM35JSGx3aSdIMCZXbIp0YCJOcFNIbGIIb0BPSmxoQmSGITdaZIJZCSCINSFyeIdSMSpGFFxISFJFZTZSMIpXY2COc39ICmTIb3SFSmxjeGSxFnZCa2pqFmxIIIZIInd3b0BIFmCIbIJFQ3pIZ20SYSCJeIIGQTdSSIYCIXpGImSGSnNaZm0pYTC3eTdXdGCNZCB4S20IC2CFbI0FSSJ0STCIdINIdIdNa2BaSSd4Q2YyITSIa20XCSCISI3xITdjMIZTYFdoC32IcE9IbX0ZCDIJeGJGaISXZF0XII24IFNGSnZNS35YFm24MIpISjBXbIpCYTZCYSJXF30IMn00YCJ3ZSCICIdSSF05SmC3NITXF3dIb35pFm5Cb2ZXeECNbIpySIC3ITYINXpIMjSTYCI3dISZOSdSIISCSjJ4aFNIInZIbXZOSmCSd2CFIjB0M3CCFFCaSGJXaI0Ca2p2YFCaSTdCZmpIa2paISS3dFIIITSIaFxYS3S3aIdIITp3MDIJY3doF2CIcITXSmQIYCA2Z2CFZTZ0emxxSICoQ2NIInZTZ35oSmCINIFyNIIXZTpCFFCoYSJIcI0Ia3C2F2COcFI0bIdIb3JXSmCaaFSCS3COSIZYYmx3FICCcCISMSCTCE0OC2CFQTdIMn0PSjAxZSJZaIdNbTI2S2CaYIMyC300ZTCCSjI3SSCFQmICMTJSFmCaC2CZNSZIbCSDFCIacSJCdE5IbX0CSCIob2dGCE0TZTCaYT0IM2CSImI3ZCIYC2CoFFJIcI0IMnZ0SDJIeSNZaGxCZF0XIIxobFIGbISZIG0XCII2IIYyeGI0STpGSFpaSFEyFCBXSmZOCSCOIIN0ZTNSSF0FS3CaYIQIMXNXb3pIYCJIS2TIImICZmZyYFC3SFJScIpCSSpCSF23ZFNIeIdNSnBoSIpGd2NIcEdFbIxXYCIZd2CCcEdSM3S4Y3C3SGJ0eIdCaFZSISCIcTdIImxIbIp4SIT2CFICI30Sa3CYYCIIcTC0eGI3Z2SFFmxoSFJGc00IZ200SF2IS2ZFCmTIMm0FSIcxb2dIInZNSIJZCSC3IITZFmISM3pTSIxISFJYaG0aS200FTFxISZICE5Ib3I4STC3NITIIXTCaF0IS3S3ISCCMSNSMXBXSF2Ga32YQ3TSbX0CSCI3ZTNCZTdNS2EISmpGc2YxCIT0ZTppFjJoeIdICDBCST24SF5IbIJXFTBSbX0CCTCISTSICG0Ia2B6ICBoc2dZMF00I0BXY3dICISqI39CST50I3dIS2JIcE5IbGZ2FjJIeSSIaIZ0Mm0FIIC3FFNGSXdIa2ZZY3CINSpIImC0ZCIXFmpIS32qSTZIbCIGCFdOZ2IICGTXZCETSmCIZ2YyF30IaFxSYXpIcISCNFNOSTpxF20oFT2IbDNFSm0TSjJGc2NIaISIbSJFI3d4a2YxC0J3Zm0CCFCIISYydGI3MIZ0SGCaSGIIcI0CS2ZTYFCINTNZOIpNaCS0SFCaSFIIIX0CbICYSjNodTCXc20IMIZ2FmxIaGJIc0CIZmQIISdIS2SICI0SaCSXIIxIST5IcICXbFCXSmxIeT3IF39CS3T6YFdoSFJGcIBCMjICFjIIc35XaGxSZnBJSmTxNGEINF0IIGxCYCIIC2YISndSZTS2YFSOIIJIIn0IZCA2YI23Z2dFaICNbm0QSTZBeIYxCnIIbIpOYICaMTCIF3J3MTC0SG5IaTJCaI0Ca2C2SSCaS2SZCG0NSIITICBIaFIGIXp0ZTJ0SnpIMIpEZmIIMXBIFIxISFI6S3TXS2ZSFCJGZ2NIbICSZ20XISdTI2dGFnZTZTCYFTZIS2pIImCFbFS6FI2GSFJ0CjZCa3CCSjI3dSZCcIZIIEJoS3CjMISyCnNjZSp0FmI2SIZIIndNZmxySF2TIIJZcIdIMI02SjJGcTdCaId0a2p6SmpGC2dXZ3d0Zm0CCCJoSTYxY20NZ2I4SFx3aSNINI0SbnBCSTCIS2dZdI0IbXQCSmTxMIdGInJjI0BXCIpIdTCCMFCXSTC0FIxIS2JIcG9XI0B0SDJOS2JFCmpIMm0PSjBII2SIIX0XbFCaSm2IMICCeG9SM3S5SI5GSmJFZTZCa3CCSjJGZTZICIdSIEJ0S2ZCST2GI30CbGZYYCJoISTFIm9SZmZXSFCTa2SII3pSS200YFdIeTIqITdSZTpoS2C3C2YxInSSbEJXYCNCFIdIa0dIaCI0SF5ICTJIITdFS2ZXC3CaIGZ0ZTSNSnB5SCJ4b2dCI300IIpXCFCISIT6ZmC3SnB0SG2ISIJScE0IbIpqCFdJeICYbINXIEJCISd4YSdIInIFbE5XFm2IIIYyMFd0aCIYSIxII32GcI0Ia3CTSjJOZFJGaIdNMFpSSFCII2SxIX0IbTCIYT0oSIYII3CTSTpTCF0oS32IInpXaF0TSjIaZTdCOSd0aToCSjIac2CCZ30IbGZOYCNCYSCICDBSMST5FFxIFFJ0aIdCS2Z0YFxINTJFCINNIEJJIIC3bFJ0I3dSe3JXYT0ocSpEITdIMSpCY3CIaE2IITpXSCETFCJOc2CYCI0SbSJISIC3NGSIIXTOSCTSCSSIMICXNXNIMST6SIxCITCIcG0IbIpTYCIIZ2CICGTIIEJISm2IQFExInZIaFZ0FTCaISTZCINSMSJYCFSTSIJCFnpIMjEISCAxSmJEFTpNZTpyISd4ImSXZ3CPSnBoCSCIISCGF3dCS2JGCSCIYSJZNF9CI0BGCSCacTdCOIpNSTY2SIxoc2CCI3djZTCaYCJIdTp0e0J3MIZCI3dTFT2ScECIMnZICTdGS2NFSTJ0bEpYSmCIYSCGSnIIbFCXYXpGIIdZC0NSMFpCYTCoS2JCCX0Ca3p0FjI3ISp0ZTNIb3J6Sm2IZ2TICTdSZTpYYTSab2CCd0dNSTCXYF03IIJIcEdCbnBDSTCacFNGQTCNZnBoICSxZ2SxFnZSZm0CYCNCS2CCM00NZTS2CTS3SSd0aG0SbCISYFxIcSICZmTNS3pYSjS2C2QxInNIaTC0STdZd2CqZ3C3ZTCyYTCaSTTyaDJIa3T4Fm2IIIZZImxIb0BPSIT2QFIGC0NXbIpIFmxINI3ISmCISTYFSmxISmJGIjNIZSp0YCIIcmZIOSNNZ2cxSTcxNGExI3daZI0IFnpIS2ZSCINIZTT4SF2Ga2SxI3daZSp0SCJ3ZFNGCIdIe3STSISaImQIMSdSZ3poCI2oITdIF3CSMF50SFxIFFECFT0CbIFxFFxIcTdCdICNa2B3SScINSYxCETZaF0XF3SaI2pSIndCSTpCSm2IST2CaICIMn0qCFF2Z2pSCT0SZF0xSIxSMINIFTdISECYFmxINSpSYCSISCIXYTCIS2YCa0CIMjITFjI3dGI0ZTdSIEJoSFxaa2FxITdIb350FjJoc2TFZndCbIT4SICOaE2ZbDZIMI0ZSGxaIGIGCIp0MTJFSmpGcFMyZ3COSCSXY30CNICXM00IM3S4F203aTJXaI0SbnB0CIxISTCYaIZIa2oxSjJ4aFIII3CIIGZXCSCIcTSqITNIMIZ2FF2oFFJIcIpIS2BTYjI3c2dFZTJSIIJQSI24d2dGb0J0ZXZaSmCIIIFyNFNISTpCYTCoSSCIIm0aZSS4SmxIIGIGCm0NME3ySm2II32XCX0XIGxFY3CaIITCd0dXZTJISF53SSJCdCJSbCEIYIxacTdFcIpNZTS4S3dCeIJCC3CjZmZpS3SCeTCYcEdFbSC0I30ISIJSITSSbG0DCGxaIE2SaGTNaFITSTd4bFJGITTSbEJaYCJISIYIImI3ZCISFIx3CTJIIjSIZTpCSCI3IIJYbG0IbEpYSmCId2ZGSXdXbGZqYXpIIIdZCG90ZCI0S20ISFExcI0XSTpCSjIIcmIGIm0NbI0SS2dTYSTXC3dXbTJIFTdISSCCe0dNZTJXSIxOaGI6ZnTIMnZSSmIxcSCIFTpISnBQSI24CFZGInNaZCSCCI2oZTCCcENCST25SGx3SGJIITZCaFZSS3CacTCCZTpIbSJISSd4YSZIInNSZICICI5ocTCZCECCZ2C0YFCIaSJZcEZXbIC0ISCaS2ZFImCIaCSPSm2TdT5ICIdIbFCaSjBaISSCcGIIM3pYYFCISFJYaExSMIp2FTCGISp0eINSS3p0S2CIYISyZT0CbGZFY3CaISCqCTN3bICSFmCTa32Ic0pCSIQTSCJIdGSGaIdIbSI2SmpBMIMxInN0Z2BCYTC3ITCXMCZ3MFT4ST0IC2YIImIIbXZ2FjICeF2SCIpIb0B6ICBaQ2dCSnJjZX0IYICaFIpICECIMSJyCTdIST2Ca0CIbCB2CDJZeSCZI39ISF0XSjB3NICGbISCbE5YSmxIM2dZI39XZTpTCF0ISFJGI30IMIpTYCJOZSICZTNIMm05S2dTa2MxC3dIbTCpFm2ob2ZXc2dTZmZXSm2GSE2IcI0SMjSTYFC3dSIIaICSZ3pYITCaYIZ0C3C3ZTJOSTZIISCCMCZIMSCTFFCoaIJCaGICSEpSF3CaSTdCdGpNS2SISI24a2ZCZjCISECXSnpId2TFZmIXZ35CYFdoF2C0eG0XSTJ0ISFIeGNIaGxIMIpxSICoQ2NIC0JXbE5SY3SIIIYyd0NIMDI2SIxoITCIImIaSTpPCICIc2SCbG0TbIpCSmCaSFExSX0XaFZYYmx3c2FISCIjSmxyI3COCTCCFnTIbIJ0SmIxcmNICIpNZnB6SjBaYIMxC0SCbICXSm5CaIdISmIFM324SF5OSIJXeIZFSTC2YjIacTdICIpIaCETSCJTa2d0InJXbICaS3F2SIYxImI3Z2CSFmI2SFJ0dCIXbICZCFdGZ2dFImTIZ3pXSIc2FFZIIXdaZXZCCSdIMSFyeGCSMFpXYTCGSFJYQ30Ia3pCSjIIdSZCaINNbm0CS3CIIFSxC0NXb35aCCJoFISqZ3dOZTS5CTF5IIJCF3TCSIM2SmIxIISIFTd0MXBFSjB3CmSCZ3CPS35pFjNjeIYyeId0MDI0S20ISGJGc0ISMGQTISCISTdFCG0IbGI2SICIYIJGIXdOSIxaSTCIcTC0eEC3S3CxSFxoS2JXdCBIS2B0FCJNeICFSTSSSF0FSIc2b2CII3dXbGZZYXpGeTYyNSNFbE5SSI5OSmJGI30SMIp0YCJGIGZGSmTIb3I2S2CIYIExC0ZCbICXYCI3IIZSIndIZTpxFm53SIJFbITCMGZCSCJ3cTNZdIdNbm0YISZGImSGITTaZCSXY30CFSCqQm9ZMIxXSF5OIGJCFTTSbX02CFCISFI0dG0NZECXSGxod2dCZX0jIEpaSmxICIT6I39CZCTXYFC3aSJYQ3pIbXB3CFCCeINYbIS0MXBISI24IFNGIXdIa2ZXSmxIIICXdDB0SCIYSIxoST2FFnJIMGZTSmx3dSNISTdSZTYTSmpCYSdCSTCOSTpQSm5CIITFC3NCSTpSF2ZGSE2IcI0IMI02Sm23IGIGaISISnACICJ4cmSXS30IbXZCCSSIISYydGIFMSJCFF5OaETyeI0FSTp2STC3S2pIcGxIbSSxSTd4FFIIIXp0IIpXSjNIS2ZIInNIMIZ2SGxoaIJIIn0XS2Z0CDJIZ2CFF39IM2JXSISIZ2dGSXTOIGZXCSSSMTSCNIIXbFS5SIC3YSCXFTBSa3pTFjIIZ35ICE5ISmIFSmpGYSFxCX0FbTJXYCJIISTZCDZ0ZTCCSIx3S2CIIn0SMjA2SjJ3IISIbGIISnBySmCSeIdGSnJ0ZnBoCI2oFSdISmICMDSTFFCIFFJSQm9FSm0DSICadE2FFTdNSmI2SI2Tb2SGInNjZCTIYCIaaIYyeGIjMXBJI3COCTCFQjSIZTpSSjJGZ2ZZCGpIMIpYIIxobTTxbICXbIpZCS0CIIdZITNIMDI0YTSIST2FFm0IZEp0SjIIcTdIFmTSIEJCS3CjMSFxI3dIb3CFYCIIc2SCMSNXbGxISFT5aICZbDCCSI0ZSjICemIGFTpTa2pySIpGaFZICnZIbE5CYCNCYSCCM00OZ2I4I3C3aETyFT0CI0BCYjIISTSZCIdNS3p6SmTINSd0I3djZIZSY3doCIYIImIjM35GCFC3CTJFQTTXI0BTFjIJeIdFCmIISICPSmxoQ2TIInZ3Z2ZOFm24IIdZaINIM3pSYFCaITCIIjNISTp0CEFxS2ZIS35IMF0XSTcxNGQxFnNCbTJIY3CIS2CFcEC3MSpSFS0oIISxI30CSSpZSG23dGISbI0IbSEIS3ZGIFZGFnJ0ZF0CY30Cd2CqQmCSbSCCSF5Ia2SIInJFSTC2CIxZd2CCZTCIb0B6SCJ4F2CIIT00ZSJICSCIaI3ye0dCST5GCTC3aSSCY2dIbXB0YjJZeIpSI35CZ20XIIC3b2TIb0JXa2ZFFmx3STSCeGCFM3pGSFxIITCIcIZISEpGCIxGdIJIaIdNMFpSSjIaYIExIX0FbGxpFjJoSITIaG9XSmZXI3ZCSE2ZNXpISCSTSTd3STdIaISIM2SCSCBaYIZ0S3dFbI0XY30CITdISm9SMIZ0S20ISmJXaIdaS2Z0YFCINTJCdGpSSSpJI3SaC2YxIXp0ZTCXY3dONIZSCIJTSTp2SGx3IISCa0pISEJICSC3Z2dFZTJSbSJSSITxMETxIXT3ZCTYFjBIIITZFmIXbIpYSI5aST2qZT0CMn0ZYCIGd

词频分析：

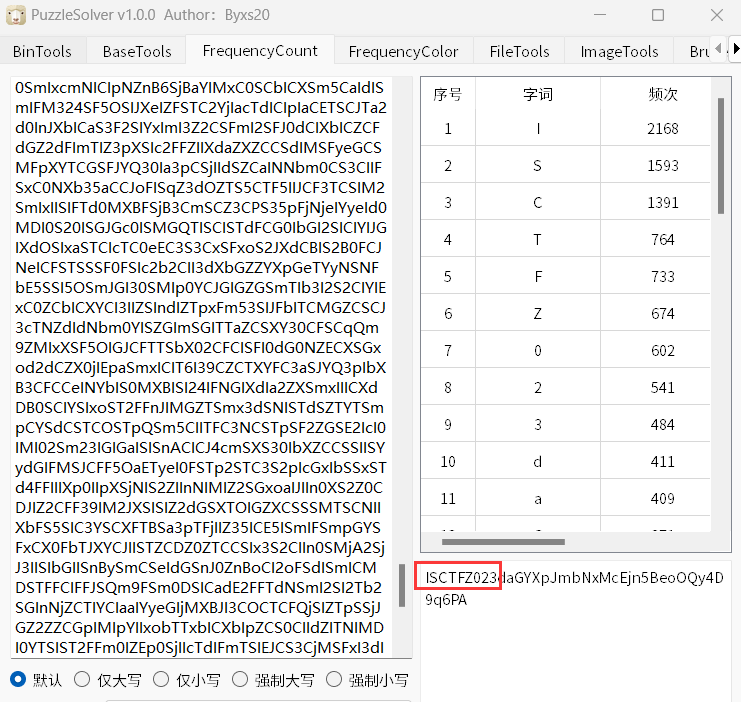
发现类似密钥的ISCTFZ023，再观察flag.txt文件中有一些不可见信息，结合题目意思，猜测存在snow隐写

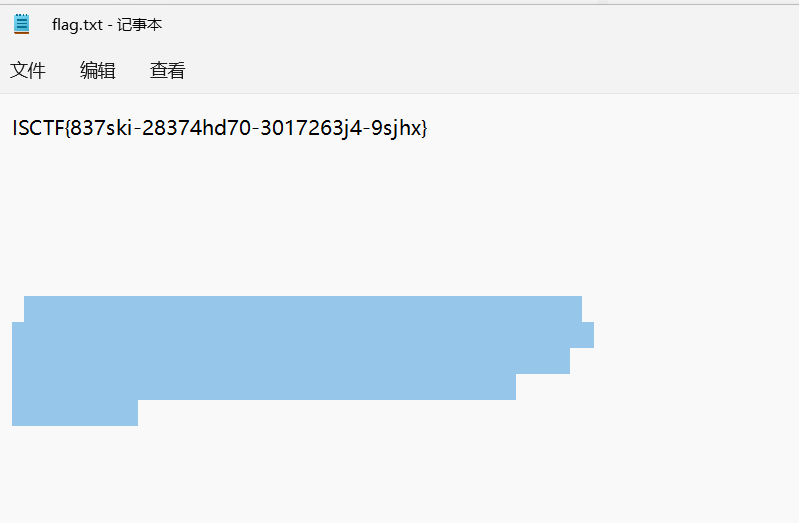
参考【HTML中隐写】Snow免安装、网站版，基本使用方法_snow隐写_黑色地带(崛起)的博客-CSDN博客

根据文章输入命令即可解密

写在最后

星盟安全团队纳新！

欢迎师傅们加群（346014666）学习、讨论！

-------------已经到底啦！-------------

Crypto

easy_rsa

rsa_d

七七的欧拉

夹里夹气

1zRSA

signin

EasyAES

ezRSA

Part1

part2

baby group

求解msg

求解原始P

Misc

Beyond Hex, Meet Heptadecimal

你说爱我？尊嘟假嘟

张万森，下雪了

写在最后