杂记(1)

记录近期做的一些题，包括强网青少赛线下赛，NCTF，强网杯，楚慧杯，强网拟态决赛的部分赛题。

由于备战期末考，时间比较紧迫，以下分析中若有不足，请师傅们指点指点◝(⑅•ᴗ•⑅)◜

强网青少赛——未解之谜

task

from Crypto.Util.number import getPrime, getRandomRange, inverse, bytes_to_long
from gmpy2 import root
from secret import flag


p = getPrime(1024)
q = getPrime(1024)
n = p * q

phi = (p - 1) * (q - 1)
d = phi - getRandomRange(2, int(root(n, 4))) // 8
e = inverse(d, phi)

print('n =', n)
print('e =', e)
print('c =', pow(bytes_to_long(flag), e, n))

"""
n = 25104277676119161522476112705793911276186101133479173238944044444464009124657009694225705909271077799809201079535406029771187080821769825464939077364642964415589149682726638069269303311285936728041400854664257359847513887226478935580304175033826156547132233021300058658354982546861556682763142936482347346981937850032206377127314298996750210542463016619202624387167346335084458869807050799087359137798417551118968333882132707224657634668232656084437165318707402672030846390316318799964502570888352016316259499484840687212162216956553959109504315812401670136366987689573854797204256680114377923495968022852465088943989
e = 20178654515985191683778773315986117381438788487541162528625194682232622732804488937715690749685871993409744005510930308420585745479669138349385107492298100706904329996211024990254138155122883012416834611836914150399764071426903891183064811037874610688800753516815651605274198703402396721086099787022825008576711822311154359274255900798872482666009298170322494751141546145941540881032818218463468104215745893024753697280199179802990999289320485792935099342229022401065822066935230288340988833699778866513151729621894378561772202838242163207916815287677576914310414398842800437151570085615904905893908276037442921399227
c = 17919859480795687548085357946533906742006563498678009884880024066719328584604178565823672582612851264338072607103147445102727569389591915368827826312868652213968050837327044813877938386742395231183072530875013974151364420171911413436696049091197432327690528295737499380220977246385029611858967823050774781344312401574401181366787200767075321779650346958885769663961952777015710540836731205786542415656103087841645510635687411784335649106356843368609597447408986641261723987501544380365356737604262721383825893578507628688434330167951610192310425417890688432557997801981742408687534970307199203734028604303069367331398
"""

关键在

d = phi - getRandomRange(2, int(root(n, 4))) // 8
e = inverse(d, phi)

设$x = $getRandomRange(2, int(root(n, 4))) // 8

$\because ed \equiv 1 \mod \phi(n)$，而且$d = \phi(n) - x$

即$e\phi(n) + e(-x) \equiv e(-x) \equiv 1 \mod \phi(n)$

$\therefore ex \equiv -1 \mod \phi(n)$

$ex = k\phi(n) - 1$

$\frac{e}{\phi(n)} = \frac{k}{x} - \frac{1}{x\phi(n)}$

$\frac{e}{n}\approx \frac{k}{x}$

$\because |\frac{e}{n}-\frac{k}{x}| \approx\frac{1}{n} < \frac{1}{2x^2}$

其中$n$是2048bit量级，而$x$是509bit量级，因此上式成立，即符合勒让德理论，因此可以连分数展开求d

需要注意的是，我们求的是$x$，但实际解密需要用$-x$解

exp:

# sage
from Crypto.Util.number import *

n = 25104277676119161522476112705793911276186101133479173238944044444464009124657009694225705909271077799809201079535406029771187080821769825464939077364642964415589149682726638069269303311285936728041400854664257359847513887226478935580304175033826156547132233021300058658354982546861556682763142936482347346981937850032206377127314298996750210542463016619202624387167346335084458869807050799087359137798417551118968333882132707224657634668232656084437165318707402672030846390316318799964502570888352016316259499484840687212162216956553959109504315812401670136366987689573854797204256680114377923495968022852465088943989
e = 20178654515985191683778773315986117381438788487541162528625194682232622732804488937715690749685871993409744005510930308420585745479669138349385107492298100706904329996211024990254138155122883012416834611836914150399764071426903891183064811037874610688800753516815651605274198703402396721086099787022825008576711822311154359274255900798872482666009298170322494751141546145941540881032818218463468104215745893024753697280199179802990999289320485792935099342229022401065822066935230288340988833699778866513151729621894378561772202838242163207916815287677576914310414398842800437151570085615904905893908276037442921399227
c = 17919859480795687548085357946533906742006563498678009884880024066719328584604178565823672582612851264338072607103147445102727569389591915368827826312868652213968050837327044813877938386742395231183072530875013974151364420171911413436696049091197432327690528295737499380220977246385029611858967823050774781344312401574401181366787200767075321779650346958885769663961952777015710540836731205786542415656103087841645510635687411784335649106356843368609597447408986641261723987501544380365356737604262721383825893578507628688434330167951610192310425417890688432557997801981742408687534970307199203734028604303069367331398

cf = continued_fraction(Integer(e) / Integer(n))

for i in range(1,10000):
    k = int(cf.numerator(i))
    d = int(cf.denominator(i))
    m = pow(c,-d,n)
    flag = long_to_bytes(int(m))
    if b"flag" in flag:
        print(f"d = {d}")
        print(i)
        print(flag)
        # flag{c30d7177-1bb7-4caf-b602-39f8d2e9792b}
        break

NCTF

Signin

# Sage
from Crypto.Util.number import *
from secret import flag
class NTRU:
    def __init__(self, N, p, q, d):
        self.debug = False

        assert q > (6*d+1)*p
        assert is_prime(N)
        assert gcd(N, q) == 1 and gcd(p, q) == 1
        self.N = N
        self.p = p
        self.q = q
        self.d = d
      
        self.R_  = PolynomialRing(ZZ,'x')
        self.Rp_ = PolynomialRing(Zmod(p),'xp')
        self.Rq_ = PolynomialRing(Zmod(q),'xq')
        x = self.R_.gen()
        xp = self.Rp_.gen()
        xq = self.Rq_.gen()
        self.R  = self.R_.quotient(x^N - 1, 'y')
        self.Rp = self.Rp_.quotient(xp^N - 1, 'yp')
        self.Rq = self.Rq_.quotient(xq^N - 1, 'yq')

        self.RpOrder = self.p^self.N - self.p
        self.RqOrder = self.q^self.N - self.q
        self.sk, self.pk = self.keyGen()

    def T(self, d1, d2):
        assert self.N >= d1+d2
        t = [1]*d1 + [-1]*d2 + [0]*(self.N-d1-d2)
        shuffle(t)
        return self.R(t)

    def lift(self, fx):
        mod = Integer(fx.base_ring()(-1)) + 1
        return self.R([Integer(x)-mod if x > mod//2 else x for x in list(fx)])

    def keyGen(self):
        fx = self.T(self.d+1, self.d)
        gx = self.T(self.d, self.d)

        Fp = self.Rp(list(fx)) ^ (-1)                         
        assert pow(self.Rp(list(fx)), self.RpOrder-1) == Fp 
        assert self.Rp(list(fx)) * Fp == 1                
        
        Fq = pow(self.Rq(list(fx)), self.RqOrder - 1)   
        assert self.Rq(list(fx)) * Fq == 1              
        
        hx = Fq * self.Rq(list(gx))

        sk = (fx, gx, Fp, Fq, hx)
        pk = hx
        return sk, pk

    def getKey(self):
        ssk = (
              self.R_(list(self.sk[0])),   
              self.R_(list(self.sk[1]))   
            )
        spk = self.Rq_(list(self.pk)) 
        return ssk, spk
     
    def pad(self,msg):
        pad_length = self.N - len(msg)
        msg += [-1 for _ in range(pad_length)]
        return msg
    
    def encode(self,msg):
        result = []
        for i in msg:
            result += [int(_) for _ in bin(i)[2:].zfill(8)]
        if len(result) < self.N:result = self.pad(result)
        result = self.R(result)
        return result


    def encrypt(self, m):
        m = self.encode(m)
        assert self.pk != None
        hx = self.pk
        mx = self.R(m)
        mx = self.Rp(list(mx))            
        mx = self.Rq(list(mx))   

        rx = self.T(self.d, self.d)
        rx = self.Rq(list(rx))
        
        e = self.p * rx * hx + mx
        return list(e)

if __name__ == '__main__':
    ntru = NTRU(N=509, p=3, q=512, d=3)
    assert len(flag) == 42
    sk, pk = ntru.getKey()
    print("fx = " , sk[0].list())
    print("gx = " , sk[1].list())
    print("hx = " , pk.list())

    e = ntru.encrypt(flag)
    print(f'e={e}')

output

fx =  [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1]
gx =  [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1]
hx =  [292, 374, 91, 384, 263, 330, 77, 497, 294, 141, 485, 464, 46, 478, 315, 100, 287, 1, 337, 477, 451, 387, 340, 370, 384, 19, 158, 440, 377, 177, 235, 340, 166, 359, 488, 332, 252, 443, 256, 453, 33, 282, 175, 18, 218, 208, 414, 147, 12, 468, 155, 34, 109, 390, 312, 472, 345, 176, 9, 184, 100, 414, 293, 366, 132, 128, 223, 242, 137, 223, 268, 259, 446, 57, 463, 344, 459, 115, 509, 510, 82, 42, 408, 139, 341, 351, 511, 339, 317, 139, 317, 297, 288, 58, 33, 120, 244, 194, 44, 128, 278, 130, 449, 282, 274, 376, 209, 240, 148, 426, 244, 319, 251, 438, 317, 166, 161, 37, 361, 468, 172, 116, 211, 64, 446, 162, 301, 447, 92, 325, 285, 4, 8, 160, 382, 365, 413, 150, 141, 323, 107, 225, 466, 93, 86, 219, 174, 198, 155, 88, 194, 259, 140, 36, 82, 462, 182, 496, 250, 337, 39, 435, 448, 365, 262, 146, 89, 283, 195, 395, 216, 159, 312, 53, 70, 485, 368, 130, 491, 474, 325, 4, 205, 1, 292, 330, 186, 66, 137, 291, 452, 236, 25, 114, 407, 125, 343, 2, 304, 267, 459, 432, 129, 21, 197, 51, 26, 342, 457, 163, 51, 52, 82, 229, 332, 72, 408, 242, 218, 286, 368, 503, 498, 434, 135, 311, 321, 205, 269, 318, 19, 119, 422, 425, 463, 368, 317, 99, 178, 390, 8, 127, 156, 27, 332, 437, 87, 187, 92, 115, 380, 54, 236, 287, 259, 386, 391, 94, 312, 454, 459, 340, 382, 424, 25, 318, 47, 249, 115, 20, 89, 82, 377, 328, 231, 298, 402, 336, 452, 264, 265, 83, 254, 156, 449, 34, 99, 412, 101, 183, 38, 142, 231, 181, 495, 6, 327, 278, 92, 452, 372, 12, 91, 102, 277, 98, 418, 22, 32, 493, 50, 374, 230, 479, 496, 6, 382, 300, 496, 157, 1, 221, 418, 381, 275, 391, 199, 472, 5, 222, 448, 377, 102, 468, 94, 35, 6, 6, 464, 452, 453, 354, 277, 425, 120, 501, 172, 222, 314, 362, 6, 105, 387, 77, 14, 112, 289, 358, 495, 350, 411, 378, 30, 89, 115, 171, 42, 32, 427, 125, 420, 486, 435, 151, 234, 416, 428, 425, 250, 142, 301, 245, 154, 338, 223, 292, 27, 194, 220, 34, 283, 255, 53, 5, 420, 134, 351, 216, 92, 242, 39, 454, 96, 239, 390, 182, 368, 463, 176, 187, 25, 122, 441, 54, 171, 426, 435, 318, 345, 166, 224, 258, 246, 349, 50, 400, 381, 236, 315, 439, 249, 201, 262, 95, 210, 327, 199, 205, 402, 175, 280, 337, 388, 205, 336, 52, 68, 364, 293, 462, 388, 354, 169, 163, 72, 374, 220, 355, 275, 36, 208, 198, 363, 369, 344, 61, 13, 230, 196, 190, 463, 351, 37, 276, 336, 110, 352, 56, 117, 376, 500, 373, 438, 309, 496, 400, 76, 169, 447, 434, 255, 456, 511, 414, 83, 369, 174, 291, 213, 227, 254, 186, 145, 402, 265, 13, 20, 212, 442]
e=[219, 149, 491, 115, 68, 464, 91, 223, 480, 506, 103, 373, 19, 52, 368, 467, 304, 380, 495, 372, 506, 318, 320, 263, 120, 126, 165, 271, 435, 378, 443, 261, 336, 381, 57, 360, 36, 155, 424, 458, 84, 80, 187, 261, 501, 279, 167, 13, 241, 85, 214, 133, 483, 374, 430, 401, 265, 127, 497, 405, 60, 34, 81, 422, 423, 200, 276, 424, 245, 437, 31, 193, 282, 154, 93, 13, 499, 190, 1, 304, 415, 189, 82, 472, 13, 488, 366, 364, 319, 121, 322, 120, 468, 134, 305, 228, 288, 284, 33, 430, 125, 366, 212, 207, 227, 201, 286, 377, 376, 57, 336, 379, 101, 461, 375, 101, 475, 126, 306, 73, 88, 1, 149, 378, 381, 129, 402, 341, 390, 57, 305, 139, 436, 101, 386, 460, 43, 468, 9, 449, 255, 184, 374, 466, 429, 167, 101, 247, 183, 159, 346, 45, 79, 192, 259, 32, 140, 151, 16, 214, 42, 450, 111, 7, 303, 286, 435, 491, 339, 248, 114, 185, 103, 81, 414, 100, 485, 428, 137, 13, 243, 202, 62, 208, 136, 376, 88, 158, 377, 404, 355, 194, 452, 373, 107, 290, 89, 489, 259, 462, 169, 235, 86, 214, 333, 472, 343, 487, 19, 371, 203, 234, 315, 339, 430, 133, 96, 161, 278, 13, 20, 87, 303, 466, 353, 139, 395, 131, 298, 85, 144, 244, 150, 488, 254, 284, 89, 300, 297, 288, 245, 439, 307, 222, 110, 343, 318, 202, 429, 81, 203, 468, 144, 140, 480, 370, 501, 14, 490, 278, 493, 390, 214, 108, 174, 150, 287, 197, 497, 374, 420, 298, 222, 188, 146, 298, 466, 459, 456, 16, 131, 253, 153, 481, 342, 498, 173, 12, 452, 197, 233, 18, 439, 332, 185, 48, 330, 4, 99, 105, 75, 306, 174, 492, 131, 39, 126, 491, 79, 145, 186, 493, 23, 230, 195, 118, 310, 173, 244, 80, 25, 502, 373, 457, 275, 282, 26, 206, 14, 181, 61, 391, 454, 417, 370, 70, 413, 389, 434, 400, 88, 417, 364, 458, 496, 425, 12, 280, 102, 265, 471, 43, 257, 327, 10, 334, 239, 344, 77, 298, 140, 287, 260, 194, 431, 65, 304, 302, 210, 393, 473, 463, 312, 255, 368, 476, 462, 390, 412, 266, 138, 410, 246, 101, 460, 307, 123, 4, 240, 502, 115, 147, 370, 241, 222, 495, 109, 51, 138, 354, 447, 282, 434, 280, 275, 404, 214, 68, 77, 167, 302, 95, 462, 16, 184, 213, 227, 130, 50, 405, 30, 353, 24, 143, 100, 163, 212, 388, 283, 252, 187, 247, 190, 163, 252, 169, 267, 363, 72, 399, 195, 215, 103, 60, 466, 318, 71, 193, 449, 65, 358, 443, 260, 253, 46, 5, 416, 115, 390, 15, 120, 384, 50, 122, 87, 428, 282, 464, 83, 80, 401, 8, 175, 457, 301, 63, 205, 402, 468, 368, 510, 488, 345, 103, 306, 387, 34, 119, 459, 43, 319, 264, 184, 406, 407, 358, 242, 42, 241, 34, 118, 477, 117, 325, 511, 499, 365, 192, 507]

题目实现了标准的NTRU密码系统，参考：NTRU密码系统 - 知乎 (zhihu.com)

该给的参数都给了

对照这文章的解密流程即可恢复

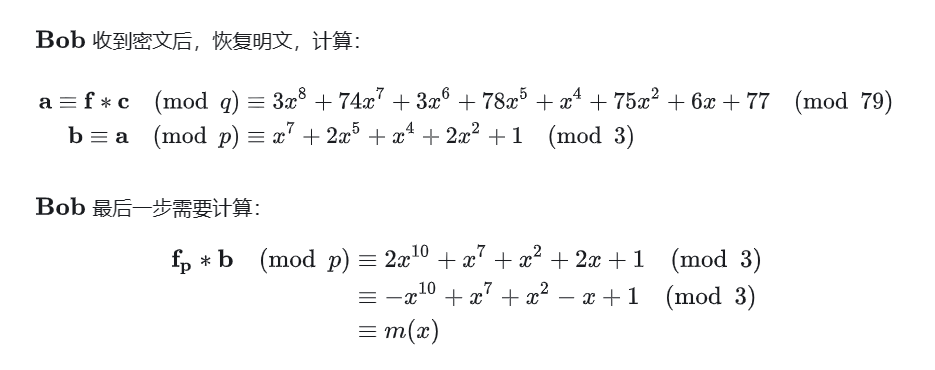
需要注意的是**计算$b\equiv a$的时候，要保证系数在$(\frac{-q}{2},\frac{q}{2})$**中

exp:

#sage
N=509
p=3
q=512
d=3
fx =  [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1]
gx =  [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1]
hx =  [292, 374, 91, 384, 263, 330, 77, 497, 294, 141, 485, 464, 46, 478, 315, 100, 287, 1, 337, 477, 451, 387, 340, 370, 384, 19, 158, 440, 377, 177, 235, 340, 166, 359, 488, 332, 252, 443, 256, 453, 33, 282, 175, 18, 218, 208, 414, 147, 12, 468, 155, 34, 109, 390, 312, 472, 345, 176, 9, 184, 100, 414, 293, 366, 132, 128, 223, 242, 137, 223, 268, 259, 446, 57, 463, 344, 459, 115, 509, 510, 82, 42, 408, 139, 341, 351, 511, 339, 317, 139, 317, 297, 288, 58, 33, 120, 244, 194, 44, 128, 278, 130, 449, 282, 274, 376, 209, 240, 148, 426, 244, 319, 251, 438, 317, 166, 161, 37, 361, 468, 172, 116, 211, 64, 446, 162, 301, 447, 92, 325, 285, 4, 8, 160, 382, 365, 413, 150, 141, 323, 107, 225, 466, 93, 86, 219, 174, 198, 155, 88, 194, 259, 140, 36, 82, 462, 182, 496, 250, 337, 39, 435, 448, 365, 262, 146, 89, 283, 195, 395, 216, 159, 312, 53, 70, 485, 368, 130, 491, 474, 325, 4, 205, 1, 292, 330, 186, 66, 137, 291, 452, 236, 25, 114, 407, 125, 343, 2, 304, 267, 459, 432, 129, 21, 197, 51, 26, 342, 457, 163, 51, 52, 82, 229, 332, 72, 408, 242, 218, 286, 368, 503, 498, 434, 135, 311, 321, 205, 269, 318, 19, 119, 422, 425, 463, 368, 317, 99, 178, 390, 8, 127, 156, 27, 332, 437, 87, 187, 92, 115, 380, 54, 236, 287, 259, 386, 391, 94, 312, 454, 459, 340, 382, 424, 25, 318, 47, 249, 115, 20, 89, 82, 377, 328, 231, 298, 402, 336, 452, 264, 265, 83, 254, 156, 449, 34, 99, 412, 101, 183, 38, 142, 231, 181, 495, 6, 327, 278, 92, 452, 372, 12, 91, 102, 277, 98, 418, 22, 32, 493, 50, 374, 230, 479, 496, 6, 382, 300, 496, 157, 1, 221, 418, 381, 275, 391, 199, 472, 5, 222, 448, 377, 102, 468, 94, 35, 6, 6, 464, 452, 453, 354, 277, 425, 120, 501, 172, 222, 314, 362, 6, 105, 387, 77, 14, 112, 289, 358, 495, 350, 411, 378, 30, 89, 115, 171, 42, 32, 427, 125, 420, 486, 435, 151, 234, 416, 428, 425, 250, 142, 301, 245, 154, 338, 223, 292, 27, 194, 220, 34, 283, 255, 53, 5, 420, 134, 351, 216, 92, 242, 39, 454, 96, 239, 390, 182, 368, 463, 176, 187, 25, 122, 441, 54, 171, 426, 435, 318, 345, 166, 224, 258, 246, 349, 50, 400, 381, 236, 315, 439, 249, 201, 262, 95, 210, 327, 199, 205, 402, 175, 280, 337, 388, 205, 336, 52, 68, 364, 293, 462, 388, 354, 169, 163, 72, 374, 220, 355, 275, 36, 208, 198, 363, 369, 344, 61, 13, 230, 196, 190, 463, 351, 37, 276, 336, 110, 352, 56, 117, 376, 500, 373, 438, 309, 496, 400, 76, 169, 447, 434, 255, 456, 511, 414, 83, 369, 174, 291, 213, 227, 254, 186, 145, 402, 265, 13, 20, 212, 442]
e = [219, 149, 491, 115, 68, 464, 91, 223, 480, 506, 103, 373, 19, 52, 368, 467, 304, 380, 495, 372, 506, 318, 320, 263, 120, 126, 165, 271, 435, 378, 443, 261, 336, 381, 57, 360, 36, 155, 424, 458, 84, 80, 187, 261, 501, 279, 167, 13, 241, 85, 214, 133, 483, 374, 430, 401, 265, 127, 497, 405, 60, 34, 81, 422, 423, 200, 276, 424, 245, 437, 31, 193, 282, 154, 93, 13, 499, 190, 1, 304, 415, 189, 82, 472, 13, 488, 366, 364, 319, 121, 322, 120, 468, 134, 305, 228, 288, 284, 33, 430, 125, 366, 212, 207, 227, 201, 286, 377, 376, 57, 336, 379, 101, 461, 375, 101, 475, 126, 306, 73, 88, 1, 149, 378, 381, 129, 402, 341, 390, 57, 305, 139, 436, 101, 386, 460, 43, 468, 9, 449, 255, 184, 374, 466, 429, 167, 101, 247, 183, 159, 346, 45, 79, 192, 259, 32, 140, 151, 16, 214, 42, 450, 111, 7, 303, 286, 435, 491, 339, 248, 114, 185, 103, 81, 414, 100, 485, 428, 137, 13, 243, 202, 62, 208, 136, 376, 88, 158, 377, 404, 355, 194, 452, 373, 107, 290, 89, 489, 259, 462, 169, 235, 86, 214, 333, 472, 343, 487, 19, 371, 203, 234, 315, 339, 430, 133, 96, 161, 278, 13, 20, 87, 303, 466, 353, 139, 395, 131, 298, 85, 144, 244, 150, 488, 254, 284, 89, 300, 297, 288, 245, 439, 307, 222, 110, 343, 318, 202, 429, 81, 203, 468, 144, 140, 480, 370, 501, 14, 490, 278, 493, 390, 214, 108, 174, 150, 287, 197, 497, 374, 420, 298, 222, 188, 146, 298, 466, 459, 456, 16, 131, 253, 153, 481, 342, 498, 173, 12, 452, 197, 233, 18, 439, 332, 185, 48, 330, 4, 99, 105, 75, 306, 174, 492, 131, 39, 126, 491, 79, 145, 186, 493, 23, 230, 195, 118, 310, 173, 244, 80, 25, 502, 373, 457, 275, 282, 26, 206, 14, 181, 61, 391, 454, 417, 370, 70, 413, 389, 434, 400, 88, 417, 364, 458, 496, 425, 12, 280, 102, 265, 471, 43, 257, 327, 10, 334, 239, 344, 77, 298, 140, 287, 260, 194, 431, 65, 304, 302, 210, 393, 473, 463, 312, 255, 368, 476, 462, 390, 412, 266, 138, 410, 246, 101, 460, 307, 123, 4, 240, 502, 115, 147, 370, 241, 222, 495, 109, 51, 138, 354, 447, 282, 434, 280, 275, 404, 214, 68, 77, 167, 302, 95, 462, 16, 184, 213, 227, 130, 50, 405, 30, 353, 24, 143, 100, 163, 212, 388, 283, 252, 187, 247, 190, 163, 252, 169, 267, 363, 72, 399, 195, 215, 103, 60, 466, 318, 71, 193, 449, 65, 358, 443, 260, 253, 46, 5, 416, 115, 390, 15, 120, 384, 50, 122, 87, 428, 282, 464, 83, 80, 401, 8, 175, 457, 301, 63, 205, 402, 468, 368, 510, 488, 345, 103, 306, 387, 34, 119, 459, 43, 319, 264, 184, 406, 407, 358, 242, 42, 241, 34, 118, 477, 117, 325, 511, 499, 365, 192, 507]

Rq.<x> = PolynomialRing(Zmod(q))
f = Rq(fx)
c = Rq(e)
Modq = x ^ N - 1
a = (f * c) % Modq
# print(f"a = {a}")
A = []
for i in a:
    A.append(int(i))

for i in range(len(A)):
    if A[i] > 256:
        A[i] -= 512
# print(A)


Rp.<x> = PolynomialRing(Zmod(p))
f = Rp(fx)
Mod = x ^ N - 1
Fp = (inverse_mod(f,Mod))
# print(Fp)
b = Rp(0)
for i in range(len(A)):
    b += A[i]*x^i
# print(b)

m = (Fp * b) % Mod
print(f"m = {m}")
flag = []
for i in m:
    flag.append(i)
# print(flag)
Flag = ""
for j in range(42):
    mm = flag[j*8:(j+1)*8]
    msg = ""
    for i in mm:
        msg += str(i)
    Flag += chr(int(msg,2))
print(Flag)
# NCTF{0e301384-a06c-11ee-959d-b39f60b9e252}

Code Infinite

首先声明这道题，由于前置知识不够扎实，导致我的理解其实很不充分，后面有时间会重新梳理思路。

util

from hashlib import sha256
from os import urandom
import random
import string

class Point:
	def __init__(self,x,y,curve, isInfinity = False):
		self.x = x % curve.p
		self.y = y % curve.p
		self.curve = curve
		self.isInfinity = isInfinity
	def __add__(self,other):
		return self.curve.add(self,other)
	def __mul__(self,other):
		return self.curve.multiply(self,other)
	def __rmul__(self,other):
		return self.curve.multiply(self,other)
	def __str__(self):
		return f"({self.x},{self.y})"
	def __eq__(self, other):
		return self.x == other.x and self.y == other.y and self.curve == other.curve

class Curve:
	def __init__(self,a,b,p):
		self.a = a%p
		self.b = b%p
		self.p = p
	def multiply(self, P:Point, k:int) -> Point:
		Q = P
		R = Point(0,0,self,isInfinity=True)
		while k > 0 :
			if (k & 1) == 1:
				R = self.add(R,Q)
			Q = self.add(Q,Q)
			k >>= 1
		return R
	def find_y(self,x):
		x = x % self.p
		y_squared = (pow(x, 3, self.p) + self.a * x + self.b) % self.p
		assert pow(y_squared, (self.p - 1) // 2, self.p) == 1, "The x coordinate is not on the curve"
		y = pow(y_squared, (self.p + 1) // 4, self.p)
		assert pow(y,2,self.p) == (pow(x, 3, self.p) + self.a * x + self.b) % self.p
		return y

	def add(self,P: Point, Q : Point) -> Point:
		if P.isInfinity:
			return Q
		elif Q.isInfinity:
			return P
		elif P.x == Q.x and P.y == (-Q.y) % self.p:
			return Point(0,0,self,isInfinity=True)
		if P.x == Q.x and P.y == Q.y:
			param = ((3*pow(P.x,2,self.p)+self.a) * pow(2*P.y,-1,self.p))
		else:
			param = ((Q.y - P.y) * pow(Q.x-P.x,-1,self.p))
		Sx =  (pow(param,2,self.p)-P.x-Q.x)%self.p
		Sy = (param * ((P.x-Sx)%self.p) - P.y) % self.p
		return Point(Sx,Sy,self)

def proof_of_work():
    random.seed(urandom(8))
    proof = ''.join([random.choice(string.ascii_letters+string.digits) for _ in range(20)])
    _hexdigest = sha256(proof.encode()).hexdigest()
    print(f"[+] sha256(XXXX+{proof[4:]}) == {_hexdigest}")
    x = input('[+] Plz tell me XXXX: ').encode()
    if len(x) != 4 or sha256(x+proof[4:].encode()).hexdigest() != _hexdigest:
        return False
    return True

task

#!/usr/local/bin/python

from util import *
from secret import flag,a,b,p
from random import randrange
from Crypto.Cipher import AES
from Crypto.Util.number import getPrime,bytes_to_long,long_to_bytes

if not proof_of_work():
	print("[!] Wrong!")
	quit()

while True:
	try:
		curve = Curve(a,b,p)
		g = randrange(1,p)
		G = Point(g,curve.find_y(g),curve)
		PK = randrange(1,p)
		pub = PK * G
		break
	except:
		continue

key = long_to_bytes(PK)[:16]
Cipher = AES.new(key,AES.MODE_ECB)
enc = Cipher.encrypt(flag)

print(f"""
=============================================
The secret is {enc.hex()} 
Alice's public key is {pub}
Now send over yours !
""")
for i in range(4):
	your_pub_key_x = int(input(f"Give me your pub key's x : \n"))
	your_pub_key_y = int(input(f"Give me your pub key's y : \n"))
	your_pub_key = Point(your_pub_key_x,your_pub_key_y,curve)
	shared_key = your_pub_key * PK
	print(f"The shared key is\n {shared_key}")

简单来说，util中实现了椭圆曲线上的加法和乘法，还有一个验证

task中，我们通过验证后，可以输入4次点(x,y)，主要任务是恢复PK

本题思路参考：Crypto趣题-曲线 | 糖醋小鸡块的blog (tangcuxiaojikuai.xyz)————————ECDH

大概是因为服务器没有对输入的点进行验证是否在曲线上，因此，我们可以改变参数b，构造一个曲线$y^2 \equiv x^3 +ax +b’$

下面具体的思路没有理清

大概就是利用CRT，用四次机会，输入四次我们曲线上的点$G_i$，服务器返回$G_i$的倍点$Q_i = PK\times G_i$

然后我们分别解4次$k_iG_i = Q_i$，最后对4个$k_i$求解CRT，即可恢复PK

因为服务器的曲线参数不变，于是我先连了4次靶机，来获得4个点，恢复出参数

如下

from Crypto.Util.number import GCD,isPrime
def recover_para(Q):
 x1,y1 = Q[0]
 x2,y2 = Q[1]
 x3,y3 = Q[2]
 x4,y4 = Q[3]
 t12_13 = ((y1**2 - x1**3)-(y2**2 - x2**3)) * (x1-x3)
 t13_12 = ((y1**2 - x1**3)-(y3**2 - x3**3)) * (x1-x2)
 k1p = t12_13-t13_12

 t12_14 = ((y1**2 - x1**3)-(y2**2 - x2**3)) * (x1-x4)
 t14_12 = ((y1**2 - x1**3)-(y4**2 - x4**3)) * (x1-x2)
 k2p = t12_14-t14_12

 p = factor(GCD(k1p,k2p))[-1][0]
 assert isPrime(int(p))

 a = ((y1^2-x1^3)-(y2^2-x2^3))/(x1-x2) % p
 b = (y1^2-x1^3-a*x1) % p

 E = EllipticCurve(GF(p),[a,b])

 assert E(Q[0])
 return E,a,b,p

Q = [
    (2845822532553776599692133610996291958841570735744741843546,5546744973172175494966318399405777490191735700856307542348),
    (164124603250334845418798190314521081977657146616868389802,5827607416298226172585153066613095195693202224870785680211),
    (3085322768139282829195896461453680669085310051891241339683,4839824814181827567238586919502670280804402058059671061077),
    (2475102402978907255506522850446484114868887359220654243314,3976026982315595141029554602740489639103543841358417228869)
]

E,a,b,p = recover_para(Q)

print("a=",a)
print("b=",b)
print("p=",p)

获得参数，发现$p \approx 192bit$，所以$PK \approx 192bit$

然后改变b，使得椭圆曲线的阶存在一些小因子

a= 6277101735386680763835789423207666416083908700390324961276
b= 2455155546008943817740293915197451784769108058161191238065
p= 6277101735386680763835789423207666416083908700390324961279

E = EllipticCurve(GF(p),[a,b])
# print(E.order())
for i in range(1,100000):
    b = i
    try:
        temp = factor(EllipticCurve(GF(p), [a, b]).order())
        print(f"b = {b}",f"temp = {temp}")
        maxp = [int(p) for p, e in temp][-1]
        if(maxp < 2 ^ 40):
            print(f"b = {b}")
            break
    except:
        pass

需要注意的是，因为只有4次交互机会，所以我们每次解的$k_i$应该在50bit左右，这就要求小因子的乘积应该在50bit左右

如下，我选择的b使得曲线能有这样的小因子，这样既保证了求解$k_iG_i = Q_i$比较快(因为这样的阶很光滑)

b = 11,a = 2**4*5*7706591*10310351				# 53bit
b = 18,a = 2**3*3*5*23*1583*17209*31120709		 # 62bit
b = 21,a = 53*83*941*23581*34812431				# 62bit
b = 24,a = 7 * 109*30949*454563497				# 54bit

最后exp:

#sage 
from Crypto.Util.number import *
from Crypto.Cipher import AES
from Pwn4Sage.pwn import *
from tqdm import *
import string
from itertools import product
import hashlib
from sympy.ntheory.modular import crt


def proof():
    table = string.ascii_letters + string.digits

    GeShi = b'[+] Plz tell me XXXX: '  # 改格式！
    
    data = sh.recvuntil(GeShi).decode()

    proof = data.split('sha256')[1]

    Xnum = proof.split('+')[0].upper().count("X")           #要爆破的数量
    tail = proof.split('+')[1].split(')')[0].strip()
    hash = proof.split('+')[1].split(')')[1].split('==')[-1].split('[')[0].strip()

    print("未知数:",Xnum)
    print(tail)
    print(hash)
    print("开始爆破")
    for i in product(table,repeat=Xnum):
        head = ''.join(i)
        t = hashlib.sha256((head + tail).encode()).hexdigest()
        if t == hash:
            print('爆破成功！结果是：', end='')
            print(head)
            sh.sendline(head.encode())
            return 


a = 6277101735386680763835789423207666416083908700390324961276
p = 6277101735386680763835789423207666416083908700390324961279
B = [(11,6356612657875280),(18,2339888236982283480),(21,3398131299244482649),(24,10734101965182239)]
modnum = []
secret = []
PUB = []

host = '115.159.221.202'                  #ip地址
port =  11112                              #端口
sh = remote(host,port)                  #建立连接  
proof()
sh.recvuntil(b"The secret is")
cipher = bytes.fromhex(str(sh.recvline().decode().strip()))
print(f"cipher = {cipher}")
sh.recvuntil(b"Now send over yours !\n")
for i in trange(4):
    b = B[i][0]
    E = EllipticCurve(Zmod(p),[a,b])
    order = E.order()
    G = E.gens()[0]
    factors = B[i][1]
    
    sendG = (order//factors)*G
    modnum.append(factors)
    sendGx = int(sendG[0])
    sendGy = int(sendG[1])
    
    sh.recvuntil(b"Give me your pub key's x :")
    sh.sendline(str(sendGx).encode())
    sh.recvuntil(b"Give me your pub key's y :")
    sh.sendline(str(sendGy).encode())
    sh.recvuntil(b"The shared key is\n")
    temp = eval(sh.recvline().strip().decode())
    print(temp)
    Qx = int(temp[0])
    Qy = int(temp[1])
    Q = E(Qx,Qy)
    PUB.append(Q)
    k = discrete_log(Q,sendG,operation = "+")
    print(f"k = {k}")
    secret.append(k)
    
    
PK = crt(modnum,secret)[0]
print(f"PK = {PK}")
key = long_to_bytes(PK)[:16]
aes = AES.new(key,AES.MODE_ECB)
flag = aes.decrypt(cipher)
print(flag)
# NCTF{ca93509d-9ecf-11ee-9b92-b025aa41becb}

赣CTF

Paillier

from Crypto.Util.number import getStrongPrime,GCD,bytes_to_long
from random import randint
flag = b"flag{xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx}"

def gen(bits):
    while True:
        try:
            p = getStrongPrime(bits//2)
            q = getStrongPrime(bits//2)
            phi = (p-1)*(q-1)
            assert GCD(p*q, phi) == 1
            break
        except:
            pass
    return p,q,phi

p,q,phi = gen(4096)
relation = pow(1949*p+2023,q,p*q)
e = bytes_to_long(flag)
n = p*p*q*q
m1 = p*q+1
m2 = randint(1,p*q)
c = pow(m1,e,n)* pow(m2,p*q,n) % n
print("pq = {}".format(p*q))
print("c = {}".format(c))
print("r = {}".format(relation))

'''
pq = 887166447166908657875261838189880924598502010532802594357792586479405303600293352901354250661651440173678984721449155150569658414460907308207395217714073465789336037528820384504682261383134149950924711017705469385976843630755333653594133550138203226251679035220402593639286098419533450127641841763263532739412752119921519469031603370689902166613111442258053360353675972164543765953155296693017036110089750056317512700539251460392822501685118151651053736001643529228257725093507504777106651318771022545536494424257325948545285947224480124270824469387763520021373564659726071920334664660638427287881128656621366437992161335475097156562366370189800926486827773369343875911013941727458484733579779987518689440390273061310030122477970154371634800517544286207542226893322249504677426768230905352021685624446085667741447943553776127246344767559462950127895715194772578266968627117192022319478447762288841148942606807267300592648345050432191106211660661975538486044324700532413628992123771986347580132637422985487775324215641630120399614206165620577557862498513625751023336154441276494811321027022075968666161204083601567420981354579585765518249333579931543871485722588207836569306920651159678633890501000411112337862727032796320667777700319
c = 323104572733056013022232486209795669816554834535601387232962336629170655850534314377617934197680759290559846935490656186083677314089429656804856335524692075372743032084131018452000127872246514430829438658543559900140854007878840361748526203998984411050117562232641090277061058838906587509258636800528603847445547938034130054858336906785685848654335600709939262479353368034082193509323294933603918116246340737911157061443282270207463561100105917304203916088760871308885091672255249534049979791578470331222906455224561104349847184035127559402743918823029257506812576223379821894308066258672451450683594036743320085094677256410814502550655295926629672064365774405226858361305878063559587655891732644666454675632155044600750031081929026668466076685284598678742892932867210546631035960182133659630156881113022786923840772277637984504620005258267988782585233487278808988499952500666966183475724382298888144869080055552509548958121952081310193858529205985575007298889289790765815033496387498756584008120132476400313134104152939600449003563325993472159269768874300428981316261923218359164567470793117504689390632939710978810213641551906532978338823420643316330940655937653381016347565948025800066537335606068590806366669159147613711722595108296517617501238810649394361783540984360800550967481778102693631148620612637261218694331865911082095074229724430736357231772418893822475389129656619563049190656052129978019794093431436182978689680711258096125364181724391940048059864568248424963697192515512824691745481055455041139683413323952422427478777508144913712466493631443481419743104115445055749214481472907347853218242035572752088863088586911967851839927488620703519887745185151057205452839656630428557432359081706642582626204620845683585079921271665513783694464226345490553425440395759713327751129225092651115897387818479920067054499945516535962600590291917909490839859244827186125356914569157371884400578544778284972543551747588182070545253302203256753412353635427924783586240203437409666455087583421435122682650900629397086322568717200715965469262221264526732434570241278318691467047049198011699661747618071924145079600200541539074616415662717381866674259250430391417176197430011943435148240516180992711773089637192808600745460407977081932525387006733024417765527436291902428861034477361566763013627884956795260111032669808711172167596733104788142220562239131262895357318086602746992514123306314802937058268304296208812601925747707823346394747245244912555520062443004568349
r = 865637930492121361886040660958095287735652100059804297239549862305074524342882218036407756195501660137614332514449671726516318012272921644431634990397955755452418355435210702607050281478215501241593800950428265623124851502962706192747580206650440857460514057532387723966581671187821458771271495725813359545478050364573058316741586000836455350643646322854627450464873523811391446102913520775230108952542654623489324912508319173605941525541092868775740020238758970696523358855304171551467374093410916441923038159303426071896161802348155237253703136258350379905869362756354512195103530352494848068900430088690695486537882796843627424321556255359200236642772594700472060253927288260231875214517350548531219877990850510060538710218821389338975073365997691494936004212511479970247940758562853029615691559463499722174608861686562660451587690321371941877852557365507747135748755958542470652752809719469470047161978745121481217418159340152676451489205085786136051301309021641406617183846328887808447131843851965391259692686700087792622136451415147478524493146973717710487616252332933063236185679743903001346951192734414668183345639614973815042497781198548651467636425872167027265577291998910747253383240028130114553850989967444499041336167318
'''

网上找了个脚本，留个坑，将来有时间复现

exp:

from Crypto.Util.number import *
import gmpy2

p =        
n = 
c = 
q = n // p
g = n + 1

# c = g^m * r^n (mod n^2) =>
# c mod n = g^m * r^n (mod n)
# And g (mod n) = 1, so g^m = 1 (mod n)  
# We got r^n = c (mod n) , and find that (φ(n),n) = 1 
phi = (p-1) * (q-1)     
# Just solve r like RSA decryption
r = pow(c%n, gmpy2.invert(n, phi), n)
# convert equation to g^m = c*r^(-n) (mod n^2)
# g^m = (n+1)^m = mn + 1 (mod n^2)
# set a = c*r^(-n) - 1, 
a = c * pow(gmpy2.invert(r,n*n), n, n*n) % (n*n) - 1
# We have mn = a (mod n^2)
# n|a , n|mn , n|n^2 , So m = a/n (mod n) => m = a/n
m = a//n 
flag = long_to_bytes(m)

if __name__ == '__main__':
    # print((a-1) % n)
    print(flag)
	# flag{i_10ve_crypto!}

强网杯

被学长带飞了，排名58！！！

Vanish的wp👉2023 强网杯 初赛 (qq.com)

speed up

计算$2^{27}!$

task

def f(x):
    res = 0
    while x:
        res += x % 10
        x //= 10
    return res

flag = flag{sha256(f(x))}

f函数是把每个十进制位的值进行求和

解法1

网站上找特殊的值

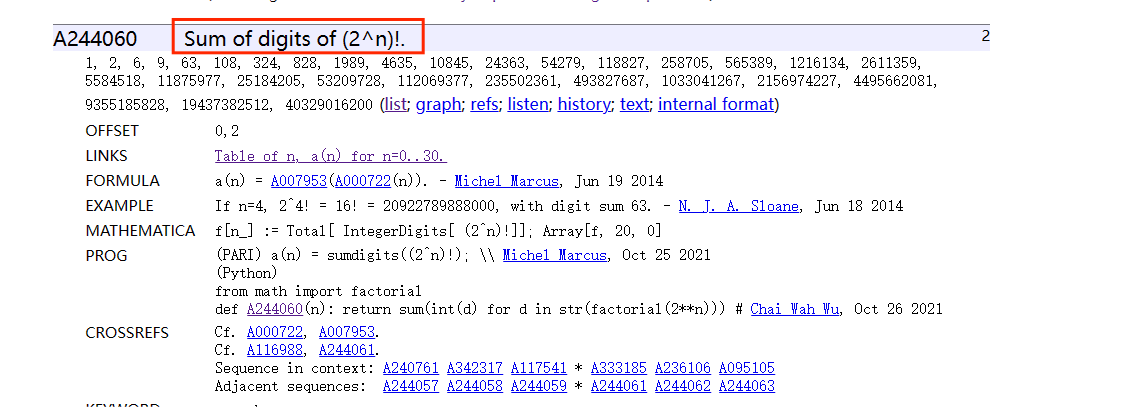
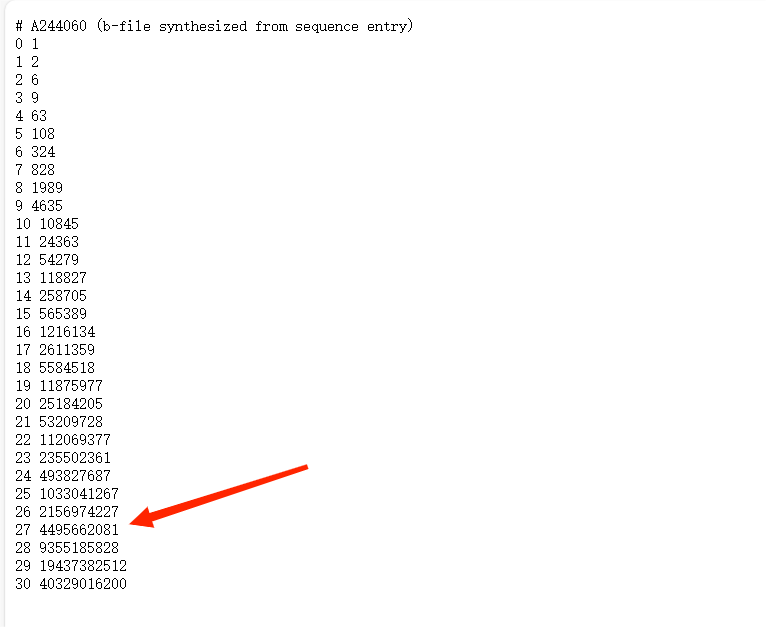
解法2

用Mathematica工具

大概7分钟出结果

工具安装教程：Mathematica安装激活极简教程 - 知乎 (zhihu.com)

exp:

import hashlib
t = 4495662081

flag = "flag{" + hashlib.sha256(str(t).encode()).hexdigest() + "}"
print(flag)

not only rsa

task

from Crypto.Util.number import bytes_to_long
from secret import flag
import os

n = 6249734963373034215610144758924910630356277447014258270888329547267471837899275103421406467763122499270790512099702898939814547982931674247240623063334781529511973585977522269522704997379194673181703247780179146749499072297334876619475914747479522310651303344623434565831770309615574478274456549054332451773452773119453059618433160299319070430295124113199473337940505806777950838270849
e = 641747
m = bytes_to_long(flag)

flag = flag + os.urandom(n.bit_length() // 8 - len(flag) - 1)
m = bytes_to_long(flag)

c = pow(m, e, n)

with open('out.txt', 'w') as f:
    print(f"{n = }", file=f)
    print(f"{e = }", file=f)
    print(f"{c = }", file=f)

out

n = 6249734963373034215610144758924910630356277447014258270888329547267471837899275103421406467763122499270790512099702898939814547982931674247240623063334781529511973585977522269522704997379194673181703247780179146749499072297334876619475914747479522310651303344623434565831770309615574478274456549054332451773452773119453059618433160299319070430295124113199473337940505806777950838270849
e = 641747
c = 730024611795626517480532940587152891926416120514706825368440230330259913837764632826884065065554839415540061752397144140563698277864414584568812699048873820551131185796851863064509294123861487954267708318027370912496252338232193619491860340395824180108335802813022066531232025997349683725357024257420090981323217296019482516072036780365510855555146547481407283231721904830868033930943

n网站分解，拿到p

发现gcd(e,phi)=e

用sagemath自带的nth_root()

#sage
from Crypto.Util.number import *

p = 91027438112295439314606669837102361953591324472804851543344131406676387779969
n = 6249734963373034215610144758924910630356277447014258270888329547267471837899275103421406467763122499270790512099702898939814547982931674247240623063334781529511973585977522269522704997379194673181703247780179146749499072297334876619475914747479522310651303344623434565831770309615574478274456549054332451773452773119453059618433160299319070430295124113199473337940505806777950838270849
e = 641747
c = 730024611795626517480532940587152891926416120514706825368440230330259913837764632826884065065554839415540061752397144140563698277864414584568812699048873820551131185796851863064509294123861487954267708318027370912496252338232193619491860340395824180108335802813022066531232025997349683725357024257420090981323217296019482516072036780365510855555146547481407283231721904830868033930943

res = Zmod(n)(c).nth_root(e, all=True)
# print(res)

for m in res:
    flag = long_to_bytes(int(m))
    if b"flag" in flag:
        print(flag)
        break
#flag{c19c3ec0-d489-4bbb-83fc-bc0419a6822a}

根据sagemath密码学 - vconlln - 博客园 (cnblogs.com)提到的

Zmod(n)(c).nth_root(t,all='True')作用是：在模$n$下求$c$的t次根

还可以求解离散对数

x=mod(5,41)
r=x.nth_root(22)

楚慧杯

so large e

task

from Crypto.Util.number import *
from Crypto.PublicKey import RSA
from flag import flag
import random

m = bytes_to_long(flag)

p = getPrime(512)
q = getPrime(512)
n = p*q
e = random.getrandbits(1024)
assert size(e)==1024
phi = (p-1)*(q-1)
assert GCD(e,phi)==1
d = inverse(e,phi)
assert size(d)==269

pub = (n, e)
PublicKey = RSA.construct(pub)
with open('pub.pem', 'wb') as f :
    f.write(PublicKey.exportKey())

c = pow(m,e,n)
print('c =',c)

print(long_to_bytes(pow(c,d,n)))


#c = 6838759631922176040297411386959306230064807618456930982742841698524622016849807235726065272136043603027166249075560058232683230155346614429566511309977857815138004298815137913729662337535371277019856193898546849896085411001528569293727010020290576888205244471943227253000727727343731590226737192613447347860

提取公钥得到n,e

发现$\frac{d}{n} = 0.26269$

多半就是boneh_durfee攻击手段

改改example()函数的delta和m即可

delta就是$\frac{d}{n}$的大小

exp:

#sage
from __future__ import print_function
import time

############################################
# Config
##########################################

"""
Setting debug to true will display more informations
about the lattice, the bounds, the vectors...
"""
debug = True

"""
Setting strict to true will stop the algorithm (and
return (-1, -1)) if we don't have a correct
upperbound on the determinant. Note that this
doesn't necesseraly mean that no solutions
will be found since the theoretical upperbound is
usualy far away from actual results. That is why
you should probably use `strict = False`
"""
strict = False

"""
This is experimental, but has provided remarkable results
so far. It tries to reduce the lattice as much as it can
while keeping its efficiency. I see no reason not to use
this option, but if things don't work, you should try
disabling it
"""
helpful_only = True
dimension_min = 7 # stop removing if lattice reaches that dimension

############################################
# Functions
##########################################

# display stats on helpful vectors
def helpful_vectors(BB, modulus):
    nothelpful = 0
    for ii in range(BB.dimensions()[0]):
        if BB[ii,ii] >= modulus:
            nothelpful += 1

    print(nothelpful, "/", BB.dimensions()[0], " vectors are not helpful")

# display matrix picture with 0 and X
def matrix_overview(BB, bound):
    for ii in range(BB.dimensions()[0]):
        a = ('%02d ' % ii)
        for jj in range(BB.dimensions()[1]):
            a += '0' if BB[ii,jj] == 0 else 'X'
            if BB.dimensions()[0] < 60:
                a += ' '
        if BB[ii, ii] >= bound:
            a += '~'
        print(a)

# tries to remove unhelpful vectors
# we start at current = n-1 (last vector)
def remove_unhelpful(BB, monomials, bound, current):
    # end of our recursive function
    if current == -1 or BB.dimensions()[0] <= dimension_min:
        return BB

    # we start by checking from the end
    for ii in range(current, -1, -1):
        # if it is unhelpful:
        if BB[ii, ii] >= bound:
            affected_vectors = 0
            affected_vector_index = 0
            # let's check if it affects other vectors
            for jj in range(ii + 1, BB.dimensions()[0]):
                # if another vector is affected:
                # we increase the count
                if BB[jj, ii] != 0:
                    affected_vectors += 1
                    affected_vector_index = jj

            # level:0
            # if no other vectors end up affected
            # we remove it
            if affected_vectors == 0:
                print("* removing unhelpful vector", ii)
                BB = BB.delete_columns([ii])
                BB = BB.delete_rows([ii])
                monomials.pop(ii)
                BB = remove_unhelpful(BB, monomials, bound, ii-1)
                return BB

            # level:1
            # if just one was affected we check
            # if it is affecting someone else
            elif affected_vectors == 1:
                affected_deeper = True
                for kk in range(affected_vector_index + 1, BB.dimensions()[0]):
                    # if it is affecting even one vector
                    # we give up on this one
                    if BB[kk, affected_vector_index] != 0:
                        affected_deeper = False
                # remove both it if no other vector was affected and
                # this helpful vector is not helpful enough
                # compared to our unhelpful one
                if affected_deeper and abs(bound - BB[affected_vector_index, affected_vector_index]) < abs(bound - BB[ii, ii]):
                    print("* removing unhelpful vectors", ii, "and", affected_vector_index)
                    BB = BB.delete_columns([affected_vector_index, ii])
                    BB = BB.delete_rows([affected_vector_index, ii])
                    monomials.pop(affected_vector_index)
                    monomials.pop(ii)
                    BB = remove_unhelpful(BB, monomials, bound, ii-1)
                    return BB
    # nothing happened
    return BB

""" 
Returns:
* 0,0   if it fails
* -1,-1 if `strict=true`, and determinant doesn't bound
* x0,y0 the solutions of `pol`
"""
def boneh_durfee(pol, modulus, mm, tt, XX, YY):
    """
    Boneh and Durfee revisited by Herrmann and May
    
    finds a solution if:
    * d < N^delta
    * |x| < e^delta
    * |y| < e^0.5
    whenever delta < 1 - sqrt(2)/2 ~ 0.292
    """

    # substitution (Herrman and May)
    PR.<u, x, y> = PolynomialRing(ZZ)
    Q = PR.quotient(x*y + 1 - u) # u = xy + 1
    polZ = Q(pol).lift()

    UU = XX*YY + 1

    # x-shifts
    gg = []
    for kk in range(mm + 1):
        for ii in range(mm - kk + 1):
            xshift = x^ii * modulus^(mm - kk) * polZ(u, x, y)^kk
            gg.append(xshift)
    gg.sort()

    # x-shifts list of monomials
    monomials = []
    for polynomial in gg:
        for monomial in polynomial.monomials():
            if monomial not in monomials:
                monomials.append(monomial)
    monomials.sort()
    
    # y-shifts (selected by Herrman and May)
    for jj in range(1, tt + 1):
        for kk in range(floor(mm/tt) * jj, mm + 1):
            yshift = y^jj * polZ(u, x, y)^kk * modulus^(mm - kk)
            yshift = Q(yshift).lift()
            gg.append(yshift) # substitution
    
    # y-shifts list of monomials
    for jj in range(1, tt + 1):
        for kk in range(floor(mm/tt) * jj, mm + 1):
            monomials.append(u^kk * y^jj)

    # construct lattice B
    nn = len(monomials)
    BB = Matrix(ZZ, nn)
    for ii in range(nn):
        BB[ii, 0] = gg[ii](0, 0, 0)
        for jj in range(1, ii + 1):
            if monomials[jj] in gg[ii].monomials():
                BB[ii, jj] = gg[ii].monomial_coefficient(monomials[jj]) * monomials[jj](UU,XX,YY)

    # Prototype to reduce the lattice
    if helpful_only:
        # automatically remove
        BB = remove_unhelpful(BB, monomials, modulus^mm, nn-1)
        # reset dimension
        nn = BB.dimensions()[0]
        if nn == 0:
            print("failure")
            return 0,0

    # check if vectors are helpful
    if debug:
        helpful_vectors(BB, modulus^mm)
    
    # check if determinant is correctly bounded
    det = BB.det()
    bound = modulus^(mm*nn)
    if det >= bound:
        print("We do not have det < bound. Solutions might not be found.")
        print("Try with highers m and t.")
        if debug:
            diff = (log(det) - log(bound)) / log(2)
            print("size det(L) - size e^(m*n) = ", floor(diff))
        if strict:
            return -1, -1
    else:
        print("det(L) < e^(m*n) (good! If a solution exists < N^delta, it will be found)")

    # display the lattice basis
    if debug:
        matrix_overview(BB, modulus^mm)

    # LLL
    if debug:
        print("optimizing basis of the lattice via LLL, this can take a long time")

    BB = BB.LLL()

    if debug:
        print("LLL is done!")

    # transform vector i & j -> polynomials 1 & 2
    if debug:
        print("looking for independent vectors in the lattice")
    found_polynomials = False
    
    for pol1_idx in range(nn - 1):
        for pol2_idx in range(pol1_idx + 1, nn):
            # for i and j, create the two polynomials
            PR.<w,z> = PolynomialRing(ZZ)
            pol1 = pol2 = 0
            for jj in range(nn):
                pol1 += monomials[jj](w*z+1,w,z) * BB[pol1_idx, jj] / monomials[jj](UU,XX,YY)
                pol2 += monomials[jj](w*z+1,w,z) * BB[pol2_idx, jj] / monomials[jj](UU,XX,YY)

            # resultant
            PR.<q> = PolynomialRing(ZZ)
            rr = pol1.resultant(pol2)

            # are these good polynomials?
            if rr.is_zero() or rr.monomials() == [1]:
                continue
            else:
                print("found them, using vectors", pol1_idx, "and", pol2_idx)
                found_polynomials = True
                break
        if found_polynomials:
            break

    if not found_polynomials:
        print("no independant vectors could be found. This should very rarely happen...")
        return 0, 0
    
    rr = rr(q, q)

    # solutions
    soly = rr.roots()

    if len(soly) == 0:
        print("Your prediction (delta) is too small")
        return 0, 0

    soly = soly[0][0]
    ss = pol1(q, soly)
    solx = ss.roots()[0][0]

    #
    return solx, soly

def example():
    ############################################
    # How To Use This Script
    ##########################################

    #
    # The problem to solve (edit the following values)
    #

    # the modulus
    N = 116518679305515263290840706715579691213922169271634579327519562902613543582623449606741546472920401997930041388553141909069487589461948798111698856100819163407893673249162209631978914843896272256274862501461321020961958367098759183487116417487922645782638510876609728886007680825340200888068103951956139343723
    e = 113449247876071397911206070019495939088171696712182747502133063172021565345788627261740950665891922659340020397229619329204520999096535909867327960323598168596664323692312516466648588320607291284630435682282630745947689431909998401389566081966753438869725583665294310689820290368901166811028660086977458571233
    # the public exponent
    # the hypothesis on the private exponent (the theoretical maximum is 0.292)
    delta = .27 # this means that d < N^delta

    #
    # Lattice (tweak those values)
    #

    # you should tweak this (after a first run), (e.g. increment it until a solution is found)
    m = 5 # size of the lattice (bigger the better/slower)

    # you need to be a lattice master to tweak these
    t = int((1-2*delta) * m)  # optimization from Herrmann and May
    X = 2*floor(N^delta)  # this _might_ be too much
    Y = floor(N^(1/2))    # correct if p, q are ~ same size

    #
    # Don't touch anything below
    #

    # Problem put in equation
    P.<x,y> = PolynomialRing(ZZ)
    A = int((N+1)/2)
    pol = 1 + x * (A + y)

    #
    # Find the solutions!
    #

    # Checking bounds
    if debug:
        print("=== checking values ===")
        print("* delta:", delta)
        print("* delta < 0.292", delta < 0.292)
        print("* size of e:", int(log(e)/log(2)))
        print("* size of N:", int(log(N)/log(2)))
        print("* m:", m, ", t:", t)

    # boneh_durfee
    if debug:
        print("=== running algorithm ===")
        start_time = time.time()

    solx, soly = boneh_durfee(pol, e, m, t, X, Y)

    # found a solution?
    if solx > 0:
        print("=== solution found ===")
        if False:
            print("x:", solx)
            print("y:", soly)

        d = int(pol(solx, soly) / e)
        print("private key found:", d)
    else:
        print("=== no solution was found ===")

    if debug:
        print(("=== %s seconds ===" % (time.time() - start_time)))

if __name__ == "__main__":
    example()

解的d = 663822343397699728953336968317794118491145998032244266550694156830036498673227937

最后解RSA

flag:DASCTF{6f4fadce-5378-d17f-3c2d-2e064db4af19}

强网拟态决赛

BadRSA

from Crypto.Util.number import *

f = open('flag.txt','rb')
m = bytes_to_long(f.readline().strip())

p = getPrime(512)
q = getPrime(512)
e = getPrime(8)
n = p*q
phi = (p-1)*(q-1)
d = inverse(e,phi)
leak = d & ((1<<265) - 1)

print(f'e = {e}')
print(f'leak = {leak}')
print(f'n = {n}')
c = pow(m,e,n)
print(f'c = {c}')

'''
e = 149
leak = 6001958312144157007304943931113872134090201010357773442954181100786589106572169
n = 88436063749749362190546240596734626745594171540325086418270903156390958817492063940459108934841028734921718351342152598224670602551497995639921650979296052943953491639892805985538785565357751736799561653032725751622522198746331856539251721033316195306373318196300612386897339425222615697620795751869751705629
c = 1206332017436789083799133504302957634035030644841294494992108068042941783794804420630684301945366528832108224264145563741764232409333108261614056154508904583078897178425071831580459193200987943565099780857889864631160747321901113496943710282498262354984634755751858251005566753245882185271726628553508627299
'''

由$ed \equiv 1 \mod \phi(n)$

即$ed = k(p-1)(q-1) + 1$

两边同时模$2^{265}$，得$ed_0 \equiv k(p-1)(q-1) + 1 \mod 2^{265}$，这里$d_0 = leak$

$\therefore ed_0 \equiv k(pq - p - q + 1) + 1 \mod 2^{265}$

再同乘$p$，得到$ed_0p \equiv knp - kp^2 - kn + kp + p \mod 2^{265}$

因为$d \approx 1023bit$

所以$k < e$

爆破$k$，解方程得到$p$的低位，然后用copper恢复$p$

exp:

from Crypto.Util.number import *
import gmpy2

e = 149
d0 = 6001958312144157007304943931113872134090201010357773442954181100786589106572169
n = 88436063749749362190546240596734626745594171540325086418270903156390958817492063940459108934841028734921718351342152598224670602551497995639921650979296052943953491639892805985538785565357751736799561653032725751622522198746331856539251721033316195306373318196300612386897339425222615697620795751869751705629
c = 1206332017436789083799133504302957634035030644841294494992108068042941783794804420630684301945366528832108224264145563741764232409333108261614056154508904583078897178425071831580459193200987943565099780857889864631160747321901113496943710282498262354984634755751858251005566753245882185271726628553508627299

for k in range(1,e):
    var("p")
    temp = e*d0*p
    f = (k*n*p - k*p^2 - k*n + k*p + p) - temp  == 0
    roots = solve_mod([f],2^265)
    if roots != []:
        for root in roots:
            plow = int(root[0])
			#print(plow)
			# 55136429770900518182274612434328885021714880080534773062619965935822096183916139
            R.<x> = PolynomialRing(Zmod(n))
            
            f1 = x*2^265 + plow
            f1 = f1.monic()
            res = f1.small_roots(X=2^247,beta=0.5,epsilon = 0.01)
            if res != []:
                print(res)
                # [188210689227294472160085325314952069542671020803828390144430392548173787275]
                p = int(res[0])*2^265 + plow
                print("p =",p)
                # p = 11158174168280917736979570452068827611755694573672250873587467083259280584739528118050085070475912733864211083865201596017044398008278425498714490994488939
                q = n // p
                d = gmpy2.invert(e,(p-1)*(q-1))
                m = pow(c,d,n)
                print(long_to_bytes(int(m)))
                # flag{827ccb0eea8a706c4c34a16891f84e7b}
                break

这里beta = 0.5是因为，对于度（即最大次方）为$d$的多项式，要求根小于$n^{\frac{\beta^2}{d} - \epsilon}$，而且要求因子$p > n^{\beta}$

此题$d = 1$，经过计算我们要求的根的上界为$2^{247}$，$\frac{247}{1024} = 0.2412$，所以取beta = 0.5可以恢复p