CTFshow元旦水友赛

发表于 更新于 分类于 阅读次数： Waline： 本文字数： 2.8k 阅读时长 ≈ 10 分钟

2024ctfshow元旦水友赛——Crypto——题解

月月的爱情故事

你知道吗。月月今天遇到了一个让他心动的女孩，她的名字叫做小雨，太幸运了。小雨是一个活泼可爱的女孩！她的笑容如同春天里的阳光。温暖了月月的心，月月第一次见到小雨是在图书馆里！事情是这样的。当时小雨正在专心致志地看书。阳光洒在她的脸上。让她看起来如同天使一般美丽！月月被小雨的美丽和才华所吸引。开始暗暗关注她。在接下来的日子里。月月开始尝试与小雨接触！和她聊天和学习。他们有着许多共同的兴趣爱好，一起度过了许多快乐的时光，渐渐地！月月发现自己对小雨产生了特殊的感情，他开始向小雨表达自己的心意，然而，小雨并没有立即接受月月的感情！她告诉月月。她曾经受过感情的伤害，需要时间来慢慢修复自己的心灵。月月尊重小雨的决定！他开始用更多的时间和精力来陪伴小雨，帮助她走出过去的阴影。在接下来的几个月里。月月和小雨的关系逐渐升温！他们一起参加了许多校园活动。一起探索了那个城市的角角落落。渐渐地！雨也开始对月月产生了感情。她发现自己越来越依赖他。越来越喜欢他。最终！小雨和月月走到了一起，他们的爱情故事成为了校园里的佳话。让同学们都羡慕不已，他们一起度过了青春岁月，一起经历了成长和进步的喜悦与挫折！他们的感情越来越深厚。也越来越稳定。在他们的恋爱过程中，月月和小雨也学会了如何相处和包容对方！他们互相理解互相支持。一起面对生活中的挑战和困难！他们的爱情让他们变得更加坚强和勇敢，也让他们感受到了生命中最美好的东西。月月相信他们能走得更远，更相信自己不会辜负小雨，当他们遭遇挫折和失败的时候！两人永远不会被打倒。这正是他们彼此爱的力量。在他们空闲的时候，月月经常带小雨出去逛街！晚上一起看电影。有一天！月月说将来他要给小雨一场最美的婚礼，小雨十分感动也十分期盼。就这样。这份约定成为了两人前进的动力。两人共同努力最终一起考上了同一所大学的研究生。两人非常开心彼此深情地看着对方似乎有说不完的情话！研究生三年他们互相帮助一起度过了人生最有意义的大学时光，毕业后两人也很轻松找到了自己心仪的企业。月月没有忘记当初的约定。是的。他要给小雨一场最美好的婚礼。终于！这一天到来了，小雨穿上月月为她定制的婚纱。他们手牵手走向了更美好的未来。场下。所有的嘉宾都为他们鼓掌和欢呼并祝福他们的爱情能够永恒长存。

VTJGc2RHVmtYMS9iVkY0NXp5dGxrZUVoZWZBcWtwSFFkTXF0VUxrMk9pYkxxNzlOSEpNbTlyUDNDdGtLckU0MQpDYUJKbU1JVmNVVlNiM0l6cEhldVd3PT0=

hint:试试摩斯吧！

根据提示，文本的标点符号替换为莫斯密码

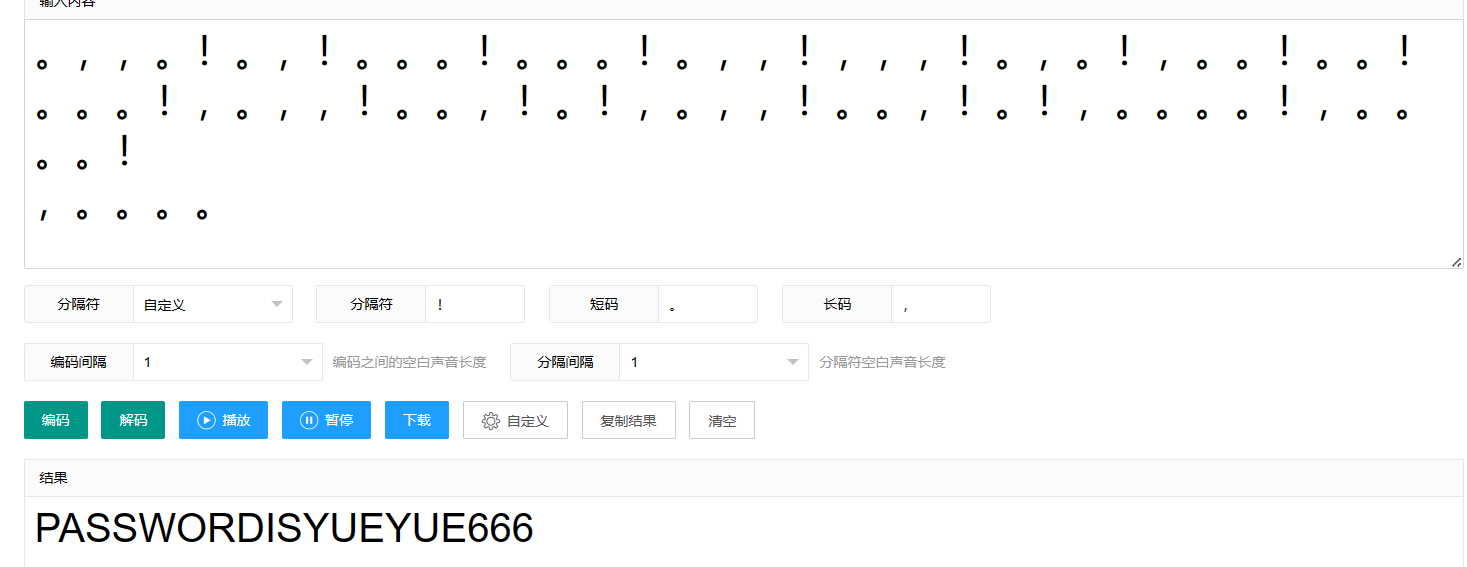
然后AES解密即可

ctfshow{W0w_th3_st0ry_s0_w0nderfu1!}

麻辣兔头又一锅

看了wp才知道

exp:

1
2
3
4
5
6
7
8
9
10
import gmpy2
c1 = [126292,165298,124522,116716,23623,21538,72802,90966,193480,77695,98618,127096,15893,65821,58966,163254,179952,134870,45821,21712,68316,87720,156070,16323,86266,148522,93678,110618,110445,136381,92706,129732,22416,177638,110110,4324,180608,3820,67750,134150,23116,116772,50573,149156,5292]
c2 = [60144,146332,165671,109800,176885,65766,76908,147004,135068,182821,123107,77538,86482,88096,101725,16475,158935,123018,42322,144694,186769,176935,59296,134856,65813,131931,144283,95814,102191,185706,55744,67711,149076,108054,135112,100344,35434,121479,14506,145222,183989,17548,38904,27832,105943]

flag = ''
for i in range(len(c1)):
    m = (gmpy2.fib(c1[i]) ^ gmpy2.fib(c2[i])) & 0xff
    flag += chr(m)
    
print(flag)

gmpy2.fib(i)用来求斐波那契数列第i个数

sign_rand

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import random
from hashlib import md5
from Crypto.Util.number import *
from flag import flag

def get_state(kbits, k):
    seed = [(random.getrandbits(kbits) >> k) & 0xfffffff for i in range(624)]
    state = (3, tuple(seed + [0]), None)
    return state


def give_gift(kbits, num):
    gift = [random.getrandbits(kbits) for i in range(num)]
    e = random.getrandbits(7)
    l_num = num - e
    s_box = list(range(num))
    random.shuffle(s_box)
    l_gift = [gift[i] for i in s_box[:l_num]]
    return (l_gift, s_box[:l_num], e)


def enc_flag(state, e):
    key = bytes_to_long(md5(long_to_bytes(state[1][e])).digest())
    enc = bytes_to_long(flag) ^ key
    return enc


kbits, k, num = random.randrange(64), random.randrange(16), random.randrange(400, 600)
state = get_state(kbits, k)
random.setstate(state)
gift = give_gift(kbits, num)
enc = enc_flag(state, gift[2])
print(gift, enc)

# ([91463260584, 97520150804, 134987178347, 134745660347, 23369346769, 88869916197, 67723104206, 132211190015, 74383600340, 57357411421, 80301226226, 2847043233, 46071508714, 76391425800, 71113777427, 12603028605, 127607785895, 82661956584, 48539405830, 131191473154, 137430688091, 48026249914, 105523652421, 58217141456, 135651011411, 37099885733, 101903983367, 117525416468, 49720139903, 123719748136, 58611168240, 68135859850, 6355615539, 23769720298, 7999623487, 19601432037, 49460687576, 34510812373, 97988805553, 120381187017, 37643325426, 79314538948, 128727827227, 41938289773, 74120986880, 29052999070, 21215042789, 76176648906, 82899209179, 90338690991, 102277220210, 109016314367, 2419923303, 75246152672, 109203867772, 87030346778, 119151949871, 134868756437, 124854798665, 122116306769, 31536426951, 82104297926, 118556737102, 78417017414, 81807286830, 24688295471, 126360674284, 8870569872, 105339369180, 61910863416, 56597235604, 50122937080, 135836683348, 75685244539, 112566491901, 86217144353, 110999080631, 91114786530, 94967775022, 52680440255, 76947914257, 133052296759, 22589975272, 104632324223, 47428022416, 106941367714, 119250845700, 80196618477, 92917756830, 52764061858, 82855761133, 26800124167, 129317288037, 44051967549, 70500283649, 165355182, 78293334339, 45001066520, 84638985033, 32566871344, 38421055041, 56145488218, 83396525174, 116762960131, 58381974438, 132249926372, 36091120717, 35213963219, 88756092150, 45288405267, 27461079382, 19589246113, 28308681656, 47161727545, 69898448282, 22959597168, 132569999975, 100557577568, 127037292334, 29708117311, 33229333831, 29311547868, 135347707719, 85435007922, 54540391811, 109544478077, 66841548339, 47159376439, 42574542524, 62176229940, 3138675000, 21267865120, 22618290315, 126018690563, 21590061225, 9799239940, 10617934652, 40956988582, 131053131140, 90043238501, 81283244185, 109338223936, 68311960398, 25088200986, 28895564195, 17646619057, 82775422880, 81522377214, 28334564831, 100791800926, 85872403124, 127915503356, 72496838376, 109007653011, 96263138881, 69693106974, 4718076407, 68334177311, 31708464646, 96111162918, 48965277868, 54931198292, 105535767797, 105680940066, 109968562576, 23573023928, 48569942163, 106967716286, 94835446653, 92803971955, 53791818332, 14453746086, 132101017989, 26361874022, 32122658200, 51724426274, 114997634813, 75838224666, 89848273104, 73619960674, 97795812498, 132466249292, 25997032367, 40732063573, 59142286405, 68524304985, 49545031400, 28044368864, 95700359624, 108201671504, 127043767055, 9384509797, 120972803416, 41782179648, 76653307257, 44056421640, 101631026937, 99078185959, 54885001820, 69316726710, 19710227322, 86035277688, 42289562955, 98051921147, 79098792488, 106490144808, 13834874, 69114014086, 4418515159, 109316722991, 92603496375, 68830244931, 111949257703, 102637560761, 5012149380, 43811237017, 4526712578, 102995188930, 9165821006, 63456393327, 68912422322, 104913358841, 108860651772, 52967416635, 84227988465, 101715630295, 26297443306, 110653579906, 91487440397, 116959430145, 83499469513, 48913630229, 76988993305, 41832173701, 13694488408, 135450931748, 39634435716, 41679152695, 126540504548, 91399825525, 99004649347, 19517357430, 8279948639, 133596449559, 1449103211, 50732184406, 52247676129, 74928416312, 64326525401, 124673786795, 92042480385, 24404916254, 99622146133, 51463314254, 36722967192, 4007778602, 39109534005, 120478575332, 99886542155, 5756463131, 91679854224, 3608646835, 35655876863, 121959477025, 20408412916, 36341277711, 43627610089, 24855949002, 128669830633, 70347508117, 9425085453, 2022963949, 5053312318, 63243834495, 21497715007, 5936366400, 44266914863, 119468825913, 91726986385, 126494307832, 93847533617, 22070910941, 20204251399, 42254244260, 60489335607, 40705184865, 80919639775, 73360223499, 132743946450, 88897376509, 103144368275, 9982808097, 131532980487, 91081435155, 78915930938, 72790758029, 120696671493, 78255313725, 13309583510, 23841020581, 116634908326, 73400462338, 57323203784, 46210923108, 41134724194, 43089395737, 118503520944, 111039189867, 99418263301, 59298127775, 45252940179, 40345195432, 16841439060, 100422187771, 65791698364, 61167532292, 30338914082, 14930863404, 4703203112, 124912009656, 9195518396, 18552364400, 7303227315, 105753747788, 3079040268, 116480022128, 1215344111, 9934249637, 76178148585, 20033461169, 87344780021, 72391242953, 129540048833, 15495213032, 49963621916, 84362224351, 97100635498, 105086571577, 51150506310, 118045067326, 65966867679, 7925108854, 131280748402, 66481282233, 107509392827, 78521145687, 35456851157, 97461157961, 30244093674, 24123083085, 27909475052, 69646113342, 131930611276, 97792139629, 135917828529, 32305782568, 59325645293, 84962280113, 74529748221, 22659244720, 54776660364, 66934871192, 14824496938, 37231294479, 102244198902, 31674646475, 128196911226, 90158594889, 121714346066, 64647669235, 105263204191, 127988380741, 130175056631, 114272442969, 135960937840, 62465712860, 32333037569, 137012433094, 92929672123, 86030288893, 73602847949, 58136148471, 118893337093, 97692245318, 99539974338, 116231441994, 32445182154, 115683286754, 114711297102, 102210385893, 7687212992, 73626254322, 242951419, 5952493527, 96817591608, 45197171621, 122928115217, 106192593180, 99889552302, 125596158762, 136959359712, 67291405558, 71974425715, 115789979144, 59321975202, 84748820897, 133266408556, 6800817333, 110678933813, 96832595879, 97681824039, 89341148630, 84626208563, 58523733456, 93000780873, 68444996084, 775177345, 17204124036, 129474447019, 73589942581, 65415043899, 131703332659, 101783987222, 61388598262, 103435807803, 104030629529, 19123072760, 63612557945, 38245223725, 54345357864, 62016904380, 34602169486, 51229280420, 66624757580, 68760378559, 131556923700, 21935621011, 36349470821, 10120892182, 25883848878, 71735922493, 62883391871, 90647098, 41388569318, 52175456448, 71822304690, 19251125978, 91308465291, 50110754397, 91050175581, 83697004380, 6165622900, 129188497722, 71424103672, 57569171583, 13220579058, 118266862549, 21791521844, 70064705221, 83120075317, 83316886784, 111745960042, 26241940218, 32402511427, 118604113535, 98847819357, 117058412964, 57680263912, 83166477192], [508, 300, 327, 517, 431, 195, 41, 162, 110, 358, 433, 105, 40, 256, 172, 50, 474, 55, 67, 284, 215, 118, 513, 98, 120, 26, 155, 298, 4, 233, 243, 267, 428, 478, 494, 226, 146, 488, 20, 113, 143, 136, 49, 236, 128, 346, 501, 264, 498, 0, 413, 30, 410, 99, 1, 220, 443, 369, 290, 374, 119, 511, 483, 199, 248, 351, 388, 335, 131, 79, 496, 245, 414, 244, 158, 451, 255, 412, 47, 473, 254, 95, 299, 462, 169, 519, 493, 12, 257, 385, 432, 417, 59, 93, 455, 324, 52, 90, 407, 288, 112, 34, 528, 29, 192, 101, 419, 203, 123, 176, 177, 167, 204, 445, 416, 485, 196, 302, 424, 425, 6, 418, 258, 17, 370, 262, 227, 326, 387, 294, 295, 174, 25, 188, 81, 408, 469, 11, 472, 80, 400, 84, 382, 448, 201, 344, 7, 502, 163, 312, 484, 349, 239, 108, 411, 315, 303, 377, 36, 383, 78, 339, 491, 271, 216, 187, 322, 140, 405, 296, 402, 516, 450, 22, 482, 361, 371, 249, 453, 64, 152, 72, 194, 66, 345, 492, 447, 58, 486, 357, 149, 200, 83, 212, 219, 504, 333, 23, 439, 376, 457, 332, 153, 348, 210, 237, 173, 359, 129, 179, 426, 71, 19, 321, 338, 444, 139, 307, 515, 88, 266, 475, 182, 323, 336, 354, 272, 384, 330, 2, 211, 446, 238, 397, 230, 278, 141, 506, 181, 70, 316, 314, 459, 235, 121, 286, 76, 518, 280, 43, 111, 62, 487, 429, 524, 364, 86, 228, 353, 275, 104, 441, 268, 13, 500, 68, 87, 109, 403, 520, 231, 391, 42, 51, 328, 253, 436, 60, 497, 313, 481, 522, 53, 61, 420, 225, 189, 325, 183, 56, 100, 229, 27, 39, 3, 184, 291, 415, 454, 75, 28, 107, 347, 421, 166, 224, 279, 16, 342, 206, 207, 171, 368, 198, 456, 464, 406, 365, 151, 320, 161, 9, 89, 479, 142, 259, 401, 232, 523, 449, 150, 218, 15, 97, 287, 133, 458, 221, 63, 185, 350, 74, 135, 404, 466, 214, 116, 507, 355, 213, 178, 318, 423, 126, 395, 465, 440, 452, 157, 366, 190, 343, 467, 247, 509, 91, 205, 114, 193, 409, 375, 269, 373, 389, 148, 69, 396, 398, 317, 145, 122, 147, 512, 32, 130, 386, 94, 435, 310, 57, 422, 308, 305, 217, 8, 154, 156, 309, 223, 44, 24, 82, 160, 392, 477, 356, 134, 54, 138, 378, 331, 379, 250, 96, 489, 306, 399, 46, 18, 283, 470, 21, 360, 209, 168, 495, 180, 514, 191, 270, 510, 381, 186, 442, 31, 390, 5, 85, 92, 363, 33, 127, 197, 285, 380, 265, 48, 352, 505, 208, 438, 329, 468, 282, 45, 159, 301, 362, 341, 65, 263, 393, 222, 521, 175, 293, 37, 490, 35], 60) 912396759652812740801869061695733452669218533249083289698313292427681899514848561025221753354562922565560034

非预期

注意到seed = [(random.getrandbits(kbits) >> k) & 0xfffffff for i in range(624)]

说明seed中的数不大于28bit

时间复杂度不多，完全可以爆破

exp:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
from tqdm import tqdm
from Crypto.Util.number import *
from hashlib import md5
import string

def dec(num):
    num = int(num)
    key = bytes_to_long(md5(long_to_bytes(num)).digest())
    m = enc ^ key
    m = long_to_bytes(m)
    try:
        flag = m.decode()
        if all(f in table for f in flag):
            print(flag)
            print(f"num = {num}")
    except:
        return

table = string.ascii_letters + '0123456789_-{}'

enc = 912396759652812740801869061695733452669218533249083289698313292427681899514848561025221753354562922565560034

for i in tqdm(range(0xfffffff+1)):
    dec(i)
# ctfshow{F2AD971D-66C2-2D1D-69D6-CE7DE2A49B35}
# num = 67529674

NOeasyRSA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
from Crypto.Util.number import long_to_bytes
from Crypto.Util.strxor import strxor
from random import randint
from flag import FLAG
 
def f(x, n):  
    return (pow(u,n,p)*x + v*(1-pow(u,n,p))*pow(1-u, -1, p)) % p  
 
p = 97201997431130462639713476119411091922677381239967611061717766639853376871260165905989218335681560177626304205941143288128749532327607316527719299945637260643711897738116821179208534292854942631428531228316344113303402450588666012800739695018334321748049518585617428717505851025279186520225325765864212731597
u = 14011530787746260724685809284106528245188320623672333581950055679051366424425259006994945665868546765648275822501035229606171697373122374288934559593175958252416643298136731105775907857798815936190074350794406666922357841091849449562922724459876362600203284195621546769313749721476449207319566681142955460891977927184371401451946649848065952527323468939007868874410618846898618148752279316070498097254384228565132693552949206926391461108714034141321700284318834819732949544823937032615318011463993204345644038210938407875147446570896826729265366024224612406740371824999201173579640264979086368843819069035017648357042
v = 16560637729264127314502582188855146263038095275553321912067588804088156431664370603746929023264744622682435376065011098909463163865218610904571775751705336266271206718700427773757241393847274601309127403955317959981271158685681135990095066557078560050980575698278958401980987514566688310172721963092100285717921465575782434632190913355536291988686994429739581469633462010143996998589435537178075521590880467628369030177392034117774853431604525531066071844562073814187461299329339694285509725214674761990940902460186665127466202741989052293452290042871514149972640901432877318075354158973805495004367245286709191395753
w = 30714296289538837760400431621661767909419746909959905820574067592409316977551664652203146506867115455464665524418603262821119202980897986798059489126166547078057148348119365709992892615014626003313040730934533283339617856938614948620116906770806796378275546490794161777851252745862081462799572448648587153412425374338967601487603800379070501278705056791472269999767679535887678042527423534392867454254712641029797659150392148648565421400107500607994226410206105774620083214215531253544274444448346065590895353139670885420838370607181375842930315910289979440845957719622069769102831263579510660283634808483329218819353
a = randint(0, 2**2048)
b = randint(0, 2**2048)
A = f(w, a)
B = f(w, b)
key = long_to_bytes(f(B, a))[:len(FLAG)]
enc = strxor(FLAG, key)
print(f"{A = }")
print(f"{B = }")
print(f"{enc = }")
 
"""
A = 19000912802080599027672447674783518419279033741329820736608320648294849832904652704615322546923683308427498322653162857743332527479657555691849627174691056234736228204031597391109766621450008024310365149769851160904834246087493085291270515883474521052340305802461028930107070785434600793548735004323108063823
B = 73344156869667785951629011239443984128961974188783039136848369309843181351498207375582387449307849089511875560536212143659712959631858144127598424003355287131145957594729789310869405545587664999655457134475561514111282513273352679348722584469527242626837672035004800949907749224093056447758969518003237425788
enc = b'\xfd\xc1\xb7\x9d"$\xc2\xb0\xb5\xee\xf89\xa4V\x8e\x17\x01K9\xbc.\x92=\x85\x80\xd4\x03\xefAl"\xbd\x8b\xcdL\xb5\xa3!'
"""

记temp = pow(1-u,-1,p)，于是有
$$
A \equiv (u^a\times(w - v\times temp) + v\times temp) \mod p
$$

$$
B \equiv (u^b\times(w - v\times temp) + v\times temp) \mod p
$$

$$
\because Key (u^a\times(B - v\times temp) + v\times temp) \mod p
$$

求得$u^a$我们即可获得$Key$

对A式进行变化得$u^a \equiv ((A - v\times temp)\times(w - v\times temp)^{-1}) \mod p$

exp:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from Crypto.Util.number import *
from Crypto.Util.strxor import strxor
import gmpy2

p = 
u = 
v = 
w = 
A = 
B = 
enc = 
temp = pow(1-u,-1,p)

tempA = (A - v*temp) % p
tempB = (B - v*temp) % p

ua = (tempA*gmpy2.invert((w - v*temp),p)) % p

key = (ua*((B - v*temp) % p) + v*temp) % p

KEY = long_to_bytes(key)[:len(enc)]
flag = strxor(enc,KEY)
print(flag)

哪位师傅知道这个是什么密码啊？

task

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import os
from Crypto.Util.number import *

F = lambda x: x * F(x-1) if x > 0 else 1
G = lambda x, y: F(x) // (F(y) * F(x-y))

def get_keys(n: int):
    p = getPrime(-11+45-14)
    print('Please wait...')
    s_list, t_list, u_list = [], [], []
    for i in range(n):
        print(f'Progress: {i+1} / {n}')
        while True:
            t, s = sorted(getPrime(101) for _ in 'NB')
            u = (G(s, t) % p) & 0xFF
            if (u != 0):
                s_list.append(s)
                t_list.append(t)
                u_list.append(u)
                break
    return (s_list, t_list, p), u_list 

FLAG = os.getenv('FLAG', 'ctfshow{never_gonna_give_you_flag}')
pubkey, privkey = get_keys(len(FLAG))
ciphertext = bytes(x ^ k for x, k in zip(FLAG.encode(), privkey))
print(f'{pubkey = }')
print(f'{ciphertext.hex() = }')

$u \equiv \frac{x!}{y! (x-y)!} \mod p \mod 255$

看到这样的形式应该想到组合数(赛时一直往阶乘想，呆瓜一个)

应用组合数取模(Lacus定理)进行快速运算

求组合数（取模）的两种方法_快速求单个组合数算法取模-CSDN博客

Lucas定理内容：
$$
C_n^m \equiv C_{\lfloor \frac{n}{p} \rfloor}^{\lfloor \frac{m}{p} \rfloor} \times C_{n \mod p}^{m \mod p} \mod p
$$

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
from Crypto.Util.number import *

pubkey = ([],)
(S_list,T_list,p) = pubkey

ciphertext = ""

def pow(a, b, m):                                       # 快速幂
    ans = 1
    a %= m
    while b:
        if b & 1:
            ans = (ans % m) * (a % m) % m
        b //= 2
        a = (a % m) * (a % m) % m
    ans %= m
    return ans

def inv(x, p):                                          # 快速求逆元
    return pow(x, p - 2, p)

def C(n, m, p):                                         # 组合数
    if m > n:
        return 0
    up, down = 1, 1
    for i in range(n - m + 1, n + 1):
        up = up * i % p
    for i in range(1, m + 1):
        down = down * i % p
    return up * inv(down, p) % p

def Lucas(n, m, p):
    if m == 0:
        return 1
    return C(n % p, m % p, p) * Lucas(n // p, m // p, p) % p

u_list = []
i = 1
for s, t in zip(S_list, T_list):
    tmp = Lucas(s, t, p)
    u = tmp & 0xFF
    print(f"Round{i}:u = {u}")
    u_list.append(u)
    i += 1
    
flag = bytes(x ^ k for x, k in zip(bytes.fromhex(ciphertext), u_list))
print(flag)
-------------已经到底啦！-------------