2024HGAME

发表于 更新于 分类于 阅读次数： Waline： 本文字数： 5k 阅读时长 ≈ 18 分钟

记录2024HGAME网络攻防大赛Crypto题解

仅分享本人的做法，并非正解

Week1

ezMath

task.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from Crypto.Util.number import *
from Crypto.Cipher import AES
import random,string
from secret import flag,y,x
def pad(x):
    return x+b'\x00'*(16-len(x)%16)
def encrypt(KEY):
    cipher= AES.new(KEY,AES.MODE_ECB)
    encrypted =cipher.encrypt(flag)
    return encrypted
D = 114514
assert x**2 - D * y**2 == 1
flag=pad(flag)
key=pad(long_to_bytes(y))[:16]
enc=encrypt(key)
print(f'enc={enc}')
#enc=b"\xce\xf1\x94\x84\xe9m\x88\x04\xcb\x9ad\x9e\x08b\xbf\x8b\xd3\r\xe2\x81\x17g\x9c\xd7\x10\x19\x1a\xa6\xc3\x9d\xde\xe7\xe0h\xed/\x00\x95tz)1\\\t8:\xb1,U\xfe\xdec\xf2h\xab`\xe5'\x93\xf8\xde\xb2\x9a\x9a"

解佩尔方程得到y

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# sage
from Crypto.Util.number import *
from Crypto.Cipher import AES

a = 1
b = 114514
enc=b"\xce\xf1\x94\x84\xe9m\x88\x04\xcb\x9ad\x9e\x08b\xbf\x8b\xd3\r\xe2\x81\x17g\x9c\xd7\x10\x19\x1a\xa6\xc3\x9d\xde\xe7\xe0h\xed/\x00\x95tz)1\\\t8:\xb1,U\xfe\xdec\xf2h\xab`\xe5'\x93\xf8\xde\xb2\x9a\x9a"
# ax^2 = by^2 + a

numTry = 1500
def solve_pell(N, numTry):
    cf = continued_fraction(sqrt(N))
    for i in range(numTry):
        denom = cf.denominator(i)
        numer = cf.numerator(i)
        if numer^2 - N * denom^2 == 1:
            return numer, denom
    return None, None

def pad(x):
    return x+b'\x00'*(16-len(x)%16)

N = b//a
x,y = solve_pell(N,numTry)
print(y)
key = pad(long_to_bytes(y))[:16]
cipher = AES.new(key,AES.MODE_ECB)
flag = cipher.decrypt(enc)
print(flag)

# hgame{G0od!_Yo3_k1ow_C0ntinued_Fra3ti0ns!!!!!!!}

ezRSA

task.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from Crypto.Util.number import *
from secret import flag
m=bytes_to_long(flag)
p=getPrime(1024)
q=getPrime(1024)
n=p*q
phi=(p-1)*(q-1)
e=0x10001
c=pow(m,e,n)
leak1=pow(p,q,n)
leak2=pow(q,p,n)

print(f'leak1={leak1}')
print(f'leak2={leak2}')
print(f'c={c}')

"""
leak1=149127170073611271968182576751290331559018441805725310426095412837589227670757540743929865853650399839102838431507200744724939659463200158012469676979987696419050900842798225665861812331113632892438742724202916416060266581590169063867688299288985734104127632232175657352697898383441323477450658179727728908669
leak2=116122992714670915381309916967490436489020001172880644167179915467021794892927977272080596641785569119134259037522388335198043152206150259103485574558816424740204736215551933482583941959994625356581201054534529395781744338631021423703171146456663432955843598548122593308782245220792018716508538497402576709461
c=10529481867532520034258056773864074017027019578041866245400647840230251661652999709715919620810933437191661180003295923273655675729588558899592524235622728816065501918076120812236580344991140980991532347991252705288633014913479970610056845543523591324177567061948922552275235486615514913932125436543991642607028689762693617305246716492783116813070355512606971626645594961850567586340389705821314842096465631886812281289843132258131809773797777049358789182212570606252509790830994263132020094153646296793522975632191912463919898988349282284972919932761952603379733234575351624039162440021940592552768579639977713099971
"""

已知
$$
leak_1 \equiv p^q \mod n
$$

$$
leak_2 \equiv q^p \mod n
$$

两个式子相乘即可得到：$leak_1 \times leak_2 \equiv p^q \times (q^q \times q^{p-q}) \mod n$

即：$leak_1 \times leak_2 \equiv n^{q} \times q^{p-q} \equiv 0 \mod n$

所以$leak_1 \times leak_2 = kn$

从 $leak_1 \equiv p^{q} \mod n$可以推出 $leak_1 \equiv p^q \equiv p \mod q$

同理 $leak_2 \equiv q^p\mod n$可以推出 $leak_2 \equiv q^p \equiv q \mod p$

通过解下面这个方程即可得到p,q
$$
leak_1 + leak_2 = p + q\
kn = p \times q
$$

Exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from Crypto.Util.number import *
import gmpy2
from sympy import symbols,solve

leak1=
leak2=
c=
e = 65537
n = leak1 * leak2

p = symbols('p')
q = symbols('q')
leak = leak1 + leak2
eq1 = p + q - leak
eq2 = p * q - n

solution = solve((eq1,eq2),(p,q))
for i in solution:
    p,q = int(i[0]),int(i[1])
    d = gmpy2.invert(e,(p-1)*(q-1))
    m = pow(c,d,n)
    print(f"p = {p}",f"q = {q}")
    print(long_to_bytes(m))
# hgame{F3rmat_l1tt1e_the0rem_is_th3_bas1s}

ezPRNG

task.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from Crypto.Util.number import *
import uuid
def PRNG(R,mask):
    nextR = (R << 1) & 0xffffffff
    i=(R&mask)&0xffffffff
    nextbit=0
    while i!=0:
        nextbit^=(i%2)
        i=i//2
    nextR^=nextbit 
    return (nextR,nextbit)

R=str(uuid.uuid4())
flag='hgame{'+R+'}'
print(flag)
R=R.replace('-','')
Rlist=[int(R[i*8:i*8+8],16) for i in range(4)]

mask=0b10001001000010000100010010001001
output=[]
for i in range(4):
    R=Rlist[i]
    out=''
    for _ in range(1000):
        (R,nextbit)=PRNG(R,mask)
        out+=str(nextbit)
    output.append(out)

print(f'output={output}')
#output=['1111110110111011110000101011010001000111111001111110100101000011110111111100010000111110110111100001001000101101011110111100010010100000011111101101110101011010111000000011110000100011101111011011000100101100110100101110001010001101101110000010001000111100101010010110110111101110011011001011111011010101011000011011000111011011111001101010111100101100110001011010010101110011101001100111000011110111000001101110000001111100000100000101111100010110111001110011010000011011110110011000001101011111111010110011010111010101001000010011110110011110110101011110111010011010010110111111010011101000110101111101111000110011111110010110000100100100101101010101110010101001101010101011110111010011101110000100101111010110101111110001111111110010000000001110011100100001011111110100111011000101001101001110010010001100011000001101000111010010000101101111101011000000101000001110001011001010010001000011000000100010010010010111010011111111011100100100100101111111001110000111110110001111001111100101001001100010', '0010000000001010111100001100011101111101111000100100111010101110010110011001011110101100011101010000001100000110000000011000000110101111111011100100110111011010000100011111000111001000101001110010110010001000110010101011110011101000011111101101011000011110001101011111000110111000011000110011100100101100111100000100100101111001011101110001011011111111011010100010111011000010010101110110100000110100000100010101000010111101001000011000000000111010010101010111101101011111011001000101000100011001100101010110110001010010001010110111011011111101011100111001101111111111010011101111010010011110011111110100110011111110110001000111100010111000101111000011011011111101110101110100111000011100001010110111100011001011010011010111000110101100110100011101101011101000111011000100110110001100110101010110010011011110000111110100111101110000100010000111100010111000010000010001111110110100001000110110100100110110010110111010011111101011110000011101010100110101011110000110101110111011010110110000010000110001', '1110110110010001011100111110111110111001111101010011001111100100001000111001101011010100010111110101110101111010111100101100010011001001011101000101011000110111000010000101001000100111010110001010000111110110111000011001100010001101000010001111111100000101111000100101000000001001001001101110000100111001110001001011010111111010111101101101001110111010111110110011001000010001010100010010110110101011100000101111100100110011110001001001111100101111001111011011010111001001111010001100110001100001100000110000011111010100101111000000101011111010000111110000101111100010000010010111010110100101010101001111100101011100011001001011000101010101001101100010110000010001110011110011100111000110101010111010011010000001100001011000011101101000000011111000101111101011110011000011011000100100110111010011001111101100101100011000101001110101111001000010110010111101110110010101101000000101001011000000001110001110000100000001001111100011010011000000011011101111101001111110001011101100000010001001010011000001', '0001101010101010100001001001100010000101010100001010001000100011101100110001001100001001110000110100010101111010110111001101011011101110000011001000100100101000011011101000111001001010011100010001010110111011100100111110111001010010111010100000100111110101110010010110100001000010010001101111001110100010001011101100111011101011101100100101011010101000101001000101110011011111110110011111111100000000011100000010011000110001000110101010001011000010101000110000101001110101010111011010010111011001010011100010101001100110000110101100010000100110101110100001101001011011110011100110011001010110100101010111110110111100000111010001111101110000000000111011011101000011001010010111001110111000100111011110100101000100011011101100011111000101110110110111111001111000000011100011000010000101001011001101110101000010101001000100110010000101001111100101000001011011010011110001101000001101111010100101001100010100000111000011110101010100011011001110001011110111010111011010101101100000110000001010010101111011']

类似2018CISCN-old Streamgame

分析代码

PRNG函数的作用是产生新的R

产生方式：

假设初始的R如下

  1. 把R的低32位作为一个整体如$R_1$，把这个整体和mask进行与操作，存为i

  2. 然后左移一位，此时R变成

  3. 然后把R从最低位，到最高位依次亦或，把最后的值记为nextbit

  4. 把nextbit作为R的最低位，此时R的值变为这样

自始至终R都是32位

因为nextbit是和i的每一位亦或而来，所以当i中有偶数个1的时候，nextbit的值为0，当i中有奇数个1的时候，nextbit的值为1

又因为i = (R & mask) & 0xffffffff，mask = 0b10001001000010000100010010001001 ,mask中第1,4,8,11,15,20,25,28,32位是1，再结合&操作的性质，我们可以推断出，nextbit的值，取决于R中第1,4,8,11,15,20,25,28,32位的值

也就可以写出表达式

nextbit = $R_1 \otimes R_4 \otimes R_8 \otimes R_{11} \otimes R_{15} \otimes R_{20} \otimes R_{25} \otimes R_{28} \otimes R_{32}$

$\therefore R_{32} = R_1 \otimes R_4 \otimes R_8 \otimes R_{11} \otimes R_{15} \otimes R_{20} \otimes R_{25} \otimes R_{28} \otimes nextbit$

根据这个状态

我们就能求$R_{32}$

再根据下一个状态，就是R30 ... R1 nextbit1 nextbit2这个状态，我们就能求$R_{31}$

以此类推即可恢复R

虽然题目给出了1000个状态，我们只需要用上前32个状态

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
output=['1111110110111011110000101011010001000111111001111110100101000011110111111100010000111110110111100001001000101101011110111100010010100000011111101101110101011010111000000011110000100011101111011011000100101100110100101110001010001101101110000010001000111100101010010110110111101110011011001011111011010101011000011011000111011011111001101010111100101100110001011010010101110011101001100111000011110111000001101110000001111100000100000101111100010110111001110011010000011011110110011000001101011111111010110011010111010101001000010011110110011110110101011110111010011010010110111111010011101000110101111101111000110011111110010110000100100100101101010101110010101001101010101011110111010011101110000100101111010110101111110001111111110010000000001110011100100001011111110100111011000101001101001110010010001100011000001101000111010010000101101111101011000000101000001110001011001010010001000011000000100010010010010111010011111111011100100100100101111111001110000111110110001111001111100101001001100010', '0010000000001010111100001100011101111101111000100100111010101110010110011001011110101100011101010000001100000110000000011000000110101111111011100100110111011010000100011111000111001000101001110010110010001000110010101011110011101000011111101101011000011110001101011111000110111000011000110011100100101100111100000100100101111001011101110001011011111111011010100010111011000010010101110110100000110100000100010101000010111101001000011000000000111010010101010111101101011111011001000101000100011001100101010110110001010010001010110111011011111101011100111001101111111111010011101111010010011110011111110100110011111110110001000111100010111000101111000011011011111101110101110100111000011100001010110111100011001011010011010111000110101100110100011101101011101000111011000100110110001100110101010110010011011110000111110100111101110000100010000111100010111000010000010001111110110100001000110110100100110110010110111010011111101011110000011101010100110101011110000110101110111011010110110000010000110001', '1110110110010001011100111110111110111001111101010011001111100100001000111001101011010100010111110101110101111010111100101100010011001001011101000101011000110111000010000101001000100111010110001010000111110110111000011001100010001101000010001111111100000101111000100101000000001001001001101110000100111001110001001011010111111010111101101101001110111010111110110011001000010001010100010010110110101011100000101111100100110011110001001001111100101111001111011011010111001001111010001100110001100001100000110000011111010100101111000000101011111010000111110000101111100010000010010111010110100101010101001111100101011100011001001011000101010101001101100010110000010001110011110011100111000110101010111010011010000001100001011000011101101000000011111000101111101011110011000011011000100100110111010011001111101100101100011000101001110101111001000010110010111101110110010101101000000101001011000000001110001110000100000001001111100011010011000000011011101111101001111110001011101100000010001001010011000001', '0001101010101010100001001001100010000101010100001010001000100011101100110001001100001001110000110100010101111010110111001101011011101110000011001000100100101000011011101000111001001010011100010001010110111011100100111110111001010010111010100000100111110101110010010110100001000010010001101111001110100010001011101100111011101011101100100101011010101000101001000101110011011111110110011111111100000000011100000010011000110001000110101010001011000010101000110000101001110101010111011010010111011001010011100010101001100110000110101100010000100110101110100001101001011011110011100110011001010110100101010111110110111100000111010001111101110000000000111011011101000011001010010111001110111000100111011110100101000100011011101100011111000101110110110111111001111000000011100011000010000101001011001101110101000010101001000100110010000101001111100101000001011011010011110001101000001101111010100101001100010100000111000011110101010100011011001110001011110111010111011010101101100000110000001010010101111011']

mask = "10001001000010000100010010001001"

def dec(key):
    R = ""
    tmp = key
    for i in range(32):
        newkey = '?'+key[:31]
        m = int(newkey[-1])^int(newkey[-4])^int(newkey[-8])^int(newkey[-11])^int(newkey[-15])^int(newkey[-20])^int(newkey[-25])^int(newkey[-28])^int(tmp[-1-i]) #这个tmp[-1-i]是求第i位对应当时lastbit的值
        R += str(m)
        key = str(m) + key[:31]
    m = hex(int(R[::-1],2))[2:]
    return m

flag = "hgame{"
for i in range(len(output)):
    mm = dec(output[i][:32])
    flag += mm
    flag += "-"
flag += "}"

print(flag)
# hgame{fbbbee82-3f43-4f91-9337-907880e4191a}

Week2

MidRSA

task.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from Crypto.Util.number import *
from secret import flag

def padding(flag):
    return flag+b'\xff'*(64-len(flag))

flag=padding(flag)
m=bytes_to_long(flag)
p=getPrime(512)
q=getPrime(512)
e=3
n=p*q
c=pow(m,e,n)
m0=m>>208

print(f'n={n}')
print(f'c={c}')
print(f'm0={m0}')

"""
n=120838778421252867808799302603972821425274682456261749029016472234934876266617266346399909705742862458970575637664059189613618956880430078774892479256301209695323302787221508556481196281420676074116272495278097275927604857336484564777404497914572606299810384987412594844071935546690819906920254004045391585427
c=118961547254465282603128910126369011072248057317653811110746611348016137361383017921465395766977129601435508590006599755740818071303929227578504412967513468921191689357367045286190040251695094706564443721393216185563727951256414649625597950957960429709583109707961019498084511008637686004730015209939219983527
m0=13292147408567087351580732082961640130543313742210409432471625281702327748963274496942276607
"""

考点：m高位泄露

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#sage
from Crypto.Util.number import long_to_bytes

n=120838778421252867808799302603972821425274682456261749029016472234934876266617266346399909705742862458970575637664059189613618956880430078774892479256301209695323302787221508556481196281420676074116272495278097275927604857336484564777404497914572606299810384987412594844071935546690819906920254004045391585427
c=118961547254465282603128910126369011072248057317653811110746611348016137361383017921465395766977129601435508590006599755740818071303929227578504412967513468921191689357367045286190040251695094706564443721393216185563727951256414649625597950957960429709583109707961019498084511008637686004730015209939219983527
m_high=13292147408567087351580732082961640130543313742210409432471625281702327748963274496942276607 
m_high <<= 208
e = 3

R.<x> = PolynomialRing(Zmod(n))
m = m_high + x
f = m^e - c
f = f.monic()

x = f.small_roots(X = 2^208,beta = 0.4)
if x:
    m = m_high + x[0]
    print(long_to_bytes(int(m)))
    # hgame{0ther_cas3s_0f_c0ppr3smith}

MidRSA revenge

task.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from Crypto.Util.number import *
from secret import flag
m=bytes_to_long(flag)
p=getPrime(1024)
q=getPrime(1024)
e=5
n=p*q
c=pow(m,e,n)
m0=m>>128

print(f'n={n}')
print(f'c={c}')
print(f'm0={m0}')

"""
n=27814334728135671995890378154778822687713875269624843122353458059697288888640572922486287556431241786461159513236128914176680497775619694684903498070577307810263677280294114135929708745988406963307279767028969515305895207028282193547356414827419008393701158467818535109517213088920890236300281646288761697842280633285355376389468360033584102258243058885174812018295460196515483819254913183079496947309574392848378504246991546781252139861876509894476420525317251695953355755164789878602945615879965709871975770823484418665634050103852564819575756950047691205355599004786541600213204423145854859214897431430282333052121
c=456221314115867088638207203034494636244706611111621723577848729096069230067958132663018625661447131501758684502639383208332844681939698124459188571813527149772292464139530736717619741704945926075632064072125361516435631121845753186559297993355270779818057702973783391589851159114029310296551701456748698914231344835187917559305440269560613326893204748127999254902102919605370363889581136724164096879573173870280806620454087466970358998654736755257023225078147018537101
m0=9999900281003357773420310681169330823266532533803905637
"""

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from Crypto.Util.number import long_to_bytes

n=27814334728135671995890378154778822687713875269624843122353458059697288888640572922486287556431241786461159513236128914176680497775619694684903498070577307810263677280294114135929708745988406963307279767028969515305895207028282193547356414827419008393701158467818535109517213088920890236300281646288761697842280633285355376389468360033584102258243058885174812018295460196515483819254913183079496947309574392848378504246991546781252139861876509894476420525317251695953355755164789878602945615879965709871975770823484418665634050103852564819575756950047691205355599004786541600213204423145854859214897431430282333052121
c=456221314115867088638207203034494636244706611111621723577848729096069230067958132663018625661447131501758684502639383208332844681939698124459188571813527149772292464139530736717619741704945926075632064072125361516435631121845753186559297993355270779818057702973783391589851159114029310296551701456748698914231344835187917559305440269560613326893204748127999254902102919605370363889581136724164096879573173870280806620454087466970358998654736755257023225078147018537101
m0=9999900281003357773420310681169330823266532533803905637
m_high = m0 << 128
e = 5

R.<x> = PolynomialRing(Zmod(n))
m = m_high + x
f = m^e - c
f = f.monic()

x = f.small_roots(X = 2^128,beta = 0.4)
if x:
    m = m_high + x[0]
    print(long_to_bytes(int(m)))
    # hgame{c0ppr3smith_St3re0typed_m3ssag3s}

backpack

task.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from Crypto.Util.number import *
import random
from secret import flag

a=[getPrime(32) for _ in range(20)]
p=random.getrandbits(32)
assert len(bin(p)[2:])==32
bag=0
for i in a:
    temp=p%2
    bag+=temp*i
    p=p>>1

enc=bytes_to_long(flag)^p

print(f'enc={enc}')
print(f'a={a}')
print(f'bag={bag}')
"""
enc=871114172567853490297478570113449366988793760172844644007566824913350088148162949968812541218339
a=[3245882327, 3130355629, 2432460301, 3249504299, 3762436129, 3056281051, 3484499099, 2830291609, 3349739489, 2847095593, 3532332619, 2406839203, 4056647633, 3204059951, 3795219419, 3240880339, 2668368499, 4227862747, 2939444527, 3375243559]
bag=45893025064
"""

背包密码一把梭，👉背包密码 | DexterJie’Blog

因为p移位之后才与flag亦或，移位后的p只有12bit，对flag的影响很小，所以可以直接long_to_bytes(enc)得到flag的大部分信息

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#sage
import libnum

enc = 871114172567853490297478570113449366988793760172844644007566824913350088148162949968812541218339
M = [3245882327, 3130355629, 2432460301, 3249504299, 3762436129, 3056281051, 3484499099, 2830291609, 3349739489, 2847095593, 3532332619, 2406839203, 4056647633, 3204059951, 3795219419, 3240880339, 2668368499, 4227862747, 2939444527, 3375243559]
S = 45893025064

n = len(M)
Ge = Matrix.identity(n)
last_row = [0 for x in range(n)]
Ge_last_row = Matrix(ZZ, 1, len(last_row), last_row)

last_col = M[:]
last_col.append(S)
Ge_last_col = Matrix(ZZ, len(last_col), 1, last_col)

Ge = Ge.stack(Ge_last_row)
Ge = Ge.augment(Ge_last_col)

X = Ge.LLL()[-1]
X = X[:-1]

p = ""
for i in X:
    if abs(i) == 1:
        p += "1"
    if abs(i) == 0:
        p += "0"
        
print(p)
m = int(p,2) ^^ enc
print(m)
flag = bytes.fromhex(hex(int(m))[2:])
print(flag)
# hgame{M@ster_0f ba3kpack_m4nag3ment!}

backpack revenge

task.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from Crypto.Util.number import *
import random
import hashlib

a=[getPrime(96) for _ in range(48)]
p=random.getrandbits(48)
assert len(bin(p)[2:])==48
flag='hgame{'+hashlib.sha256(str(p).encode()).hexdigest()+'}'

bag=0
for i in a:
    temp=p%2
    bag+=temp*i
    p=p>>1

print(f'a={a}')
print(f'bag={bag}')

"""
a=[74763079510261699126345525979, 51725049470068950810478487507, 47190309269514609005045330671, 64955989640650139818348214927, 68559937238623623619114065917, 72311339170112185401496867001, 70817336064254781640273354039, 70538108826539785774361605309, 43782530942481865621293381023, 58234328186578036291057066237, 68808271265478858570126916949, 61660200470938153836045483887, 63270726981851544620359231307, 42904776486697691669639929229, 41545637201787531637427603339, 74012839055649891397172870891, 56943794795641260674953676827, 51737391902187759188078687453, 49264368999561659986182883907, 60044221237387104054597861973, 63847046350260520761043687817, 62128146699582180779013983561, 65109313423212852647930299981, 66825635869831731092684039351, 67763265147791272083780752327, 61167844083999179669702601647, 55116015927868756859007961943, 52344488518055672082280377551, 52375877891942312320031803919, 69659035941564119291640404791, 52563282085178646767814382889, 56810627312286420494109192029, 49755877799006889063882566549, 43858901672451756754474845193, 67923743615154983291145624523, 51689455514728547423995162637, 67480131151707155672527583321, 59396212248330580072184648071, 63410528875220489799475249207, 48011409288550880229280578149, 62561969260391132956818285937, 44826158664283779410330615971, 70446218759976239947751162051, 56509847379836600033501942537, 50154287971179831355068443153, 49060507116095861174971467149, 54236848294299624632160521071, 64186626428974976108467196869]
bag=1202548196826013899006527314947
"""

普通的LLL规约出的结果并不好,换用BKZ

block_size越大，效果越好，运行越慢

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import libnum
import hashlib
from math import *

M = [74763079510261699126345525979, 51725049470068950810478487507, 47190309269514609005045330671, 64955989640650139818348214927, 68559937238623623619114065917, 72311339170112185401496867001, 70817336064254781640273354039, 70538108826539785774361605309, 43782530942481865621293381023, 58234328186578036291057066237, 68808271265478858570126916949, 61660200470938153836045483887, 63270726981851544620359231307, 42904776486697691669639929229, 41545637201787531637427603339, 74012839055649891397172870891, 56943794795641260674953676827, 51737391902187759188078687453, 49264368999561659986182883907, 60044221237387104054597861973, 63847046350260520761043687817, 62128146699582180779013983561, 65109313423212852647930299981, 66825635869831731092684039351, 67763265147791272083780752327, 61167844083999179669702601647, 55116015927868756859007961943, 52344488518055672082280377551, 52375877891942312320031803919, 69659035941564119291640404791, 52563282085178646767814382889, 56810627312286420494109192029, 49755877799006889063882566549, 43858901672451756754474845193, 67923743615154983291145624523, 51689455514728547423995162637, 67480131151707155672527583321, 59396212248330580072184648071, 63410528875220489799475249207, 48011409288550880229280578149, 62561969260391132956818285937, 44826158664283779410330615971, 70446218759976239947751162051, 56509847379836600033501942537, 50154287971179831355068443153, 49060507116095861174971467149, 54236848294299624632160521071, 64186626428974976108467196869]
S = 1202548196826013899006527314947

n = len(M)
d = n / log2(max(M))
assert d < 0.9408, f"Density should be less than 0.9408 but was {d}."

Ge = Matrix(ZZ,n+1,n+1)
for i in range(n):
    Ge[i,i] = 1
    Ge[i,n] = M[i]
Ge[n,n] = -S

X = Ge.BKZ(block_size=30)

for line in X:
    if line[-1] == 0:
        x = [abs(i) for i in line[:-1]]
        if set(x).issubset([0, 1]):
            x = ''.join([str(i) for i in x[::-1]])
            print(f"x = {x}")
            p = int(x,2)
            print(f"p = {p}")
            # 268475474669857
            flag = 'hgame{' + hashlib.sha256(str(p).encode()).hexdigest() + '}'
            print(flag)
            # hgame{04b1d0b0fb805a70cda94348ec5a33f900d4fd5e9c45e765161c434fa0a49991}

babyRSA

task.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from Crypto.Util.number import *
from secret import flag,e
m=bytes_to_long(flag)
p=getPrime(64)
q=getPrime(256)
n=p**4*q
k=getPrime(16)
gift=pow(e+114514+p**k,0x10001,p)
c=pow(m,e,n)
print(f'p={p}')
print(f'q={q}')
print(f'c={c}')
print(f'gift={gift}')
"""
p=14213355454944773291
q=61843562051620700386348551175371930486064978441159200765618339743764001033297
c=105002138722466946495936638656038214000043475751639025085255113965088749272461906892586616250264922348192496597986452786281151156436229574065193965422841
gift=9751789326354522940
"""

$$
gift \equiv (e + 114514 + p^k)^{65537} \mod p
$$

$$
\therefore gift \equiv (e + 114514)^{65537} \mod p
$$

解一次RSA得到$e$

发现e和$\phi(n) = p^3(p-1)(q-1)$不互素

用nthroot处理

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# sage
from Crypto.Util.number import *
import gmpy2

p = 14213355454944773291
q = 61843562051620700386348551175371930486064978441159200765618339743764001033297
c = 105002138722466946495936638656038214000043475751639025085255113965088749272461906892586616250264922348192496597986452786281151156436229574065193965422841
gift = 9751789326354522940

n = p**4*q
d = gmpy2.invert(65537,p-1)
temp = pow(gift,d,p)
e = temp - 114514
phi = p**3*(p-1)*(q-1)
# print(gmpy2.gcd(e,phi))
# 73561
res = Zmod(n)(c).nth_root(e, all=True)

for m in res:
    flag = long_to_bytes(int(m))
    if b"hgame" in flag:
        print(flag)
        break
# hgame{Ad1eman_Mand3r_Mi11er_M3th0d}

Week3

exRSA

task.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from Crypto.Util.number import *
from secret import flag
m=bytes_to_long(flag)
p=getStrongPrime(1024)
q=getStrongPrime(1024)
phi=(p-1)*(q-1)
e1=inverse(getPrime(768),phi)
e2=inverse(getPrime(768),phi)
e3=inverse(getPrime(768),phi)
n=p*q
c=pow(m,0x10001,n)
print(f'e1={e1}')
print(f'e2={e2}')
print(f'e3={e3}')
print(f'c={c}')
print(f'n={n}')

"""
e1=5077048237811969427473111225370876122528967447056551899123613461792688002896788394304192917610564149766252232281576990293485239684145310876930997918960070816968829150376875953405420809586267153171717496198336861089523701832098322284501931142889817575816761705044951705530849327928849848158643030693363143757063220584714925893965587967042137557807261154117916358519477964645293471975063362050690306353627492980861008439765365837622657977958069853288056307253167509883258122949882277021665317807253308906355670472172346171177267688064959397186926103987259551586627965406979118193485527520976748490728460167949055289539
e2=12526848298349005390520276923929132463459152574998625757208259297891115133654117648215782945332529081365273860316201130793306570777735076534772168999705895641207535303839455074003057687810381110978320988976011326106919940799160974228311824760046370273505511065619268557697182586259234379239410482784449815732335294395676302226416863709340032987612715151916084291821095462625821023133560415325824885347221391496937213246361736361270846741128557595603052713612528453709948403100711277679641218520429878897565655482086410576379971404789212297697553748292438183065500993375040031733825496692797699362421010271599510269401
e3=12985940757578530810519370332063658344046688856605967474941014436872720360444040464644790980976991393970947023398357422203873284294843401144065013911463670501559888601145108651961098348250824166697665528417668374408814572959722789020110396245076275553505878565603509466220710219260037783849276475397283421068716088638186994778153542817681963059581651103563578804145156157584336712678882995685632615686853980176047683326974283896343322981521150211317597571554542488921290158122634140571148036732893808064119048328855134054709120877895941670166421664806186710346824494054783025733475898081247824887967550418509038276279
c=1414176060152301842110497098024597189246259172019335414900127452098233943041825926028517437075316294943355323947458928010556912909139739282924255506647305696872907898950473108556417350199783145349691087255926287363286922011841143339530863300198239231490707393383076174791818994158815857391930802936280447588808440607415377391336604533440099793849237857247557582307391329320515996021820000355560514217505643587026994918588311127143566858036653315985177551963836429728515745646807123637193259859856630452155138986610272067480257330592146135108190083578873094133114440050860844192259441093236787002715737932342847147399
n=17853303733838066173110417890593704464146824886316456780873352559969742615755294466664439529352718434399552818635352768033531948009737170697566286848710832800426311328560924133698481653594007727877031506265706341560810588064209681809146597572126173303463125668183837840427667101827234752823747483792944536893070188010357644478512143332014786539698535220139784440314481371464053954769822738407808161946943216714729685820896972467020893493349051243983390018762076812868678098172416465691550285372846402991995794349015838868221686216396597327273110165922789814315858462049706255254066724012925815100434953821856854529753
"""

3对ed，扩展维纳攻击

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
import gmpy2
import libnum
isdigit = lambda x: ord('0') <= ord(x) <= ord('9')

def my_permutations(g, n):
    sub = []
    res = []
    def dfs(s, prev):
        if len(s) == n:
            res.append(s[::])
        for i in g:
            if i in s or i < prev:
                continue
            s.append(i)
            dfs(s, max(prev, i))
            s.remove(i)
    dfs(sub, 0)
    return res

class X3NNY(object):
    def __init__(self, exp1, exp2):
        self.exp1 = exp1
        self.exp2 = exp2
    
    def __mul__(self, b):
        return X3NNY(self.exp1 * b.exp1, self.exp2 * b.exp2)

    def __repr__(self):
        return '%s = %s' % (self.exp1.expand().collect_common_factors(), self.exp2)

class X_Complex(object):
    def __init__(self, exp):
        i = 0
        s = '%s' % exp
        while i < len(s):
            if isdigit(s[i]):
                num = 0
                while i < len(s) and isdigit(s[i]):
                    num = num*10 + int(s[i])
                    i += 1
                if i >= len(s):
                    self.b = num
                elif s[i] == '*':
                    self.a = num
                    i += 2
                elif s[i] == '/':
                    i += 1
                    r = 0
                    while i < len(s) and isdigit(s[i]):
                        r = r*10 + int(s[i])
                        i += 1
                    self.b = num/r
            else:
                i += 1
        if not hasattr(self, 'a'):
            self.a = 1
        if not hasattr(self, 'b'):
            self.b = 0

def WW(e, d, k, g, N, s):
    return X3NNY(e*d*g-k*N, g+k*s)
def GG(e1, e2, d1, d2, k1, k2):
    return X3NNY(e1*d1*k2- e2*d2*k1, k2 - k1)

def W(i):
    e = eval("e%d" % i)
    d = eval("d%d" % i)
    k = eval("k%d" % i)
    return WW(e, d, k, g, N, s)

def G(i, j):
    e1 = eval("e%d" % i)
    d1 = eval("d%d" % i)
    k1 = eval("k%d" % i)
    
    e2 = eval("e%d" % j)
    d2 = eval("d%d" % j)
    k2 = eval("k%d" % j)
    
    return GG(e1, e2, d1, d2, k1, k2)

def R(e, sn): # min u max v
    ret = X3NNY(1, 1)
    n = max(e)
    nn = len(e)
    l = set(i for i in range(1, n+1))
    debug = ''
    u, v = 0, 0
    for i in e:
        if i == 1:
            ret *= W(1)
            debug += 'W(%d)' % i
            nn -= 1
            l.remove(1)
            u += 1
        elif i > min(l) and len(l) >= 2*nn:
            ret *= G(min(l), i)
            nn -= 1
            debug += 'G(%d, %d)' % (min(l), i)
            l.remove(min(l))
            l.remove(i)
            v += 1
        else:
            ret *= W(i)
            l.remove(i)
            debug += 'W(%d)' % i
            nn -= 1
            u += 1
    # print(debug, end = ' ')
    return ret, u/2 + (sn - v) * a

def H(n):
    if n == 0:
        return [0]
    if n == 2:
        return [(), (1,), (2,), (1, 2)]
    ret = []
    for i in range(3, n+1):
        ret.append((i,))
        for j in range(1, i):
            for k in my_permutations(range(1, i), j):
                ret.append(tuple(k + [i]))
    return H(2) + ret
    
def CC(exp, n):
    cols = [0 for i in range(1<<n)]
    
    # split exp
    texps = ('%s' % exp.exp1.expand()).strip().split(' - ')
    ops = []
    exps = []
    for i in range(len(texps)):
        if texps[i].find(' + ') != -1:
            tmp = texps[i].split(' + ')
            ops.append(0)
            exps.append(tmp[0])
            for i in range(1, len(tmp)):
                ops.append(1)
                exps.append(tmp[i])
        else:
            ops.append(0)
            exps.append(texps[i])
    if exps[0][0] == '-':
        for i in range(len(exps)):
            ops[i] = 1-ops[i]
        exps[0] = exps[0][1:]
    else:
        ops[0] = 1
    # find e and N
    l = []
    for i in range(len(exps)):
        tmp = 1 if ops[i] else -1
        en = []
        j = 0
        while j < len(exps[i]):
            if exps[i][j] == 'e':
                num = 0
                j += 1
                while isdigit(exps[i][j]):
                    num = num*10 + int(exps[i][j])
                    j += 1
                tmp *= eval('e%d' % num)
                en.append(num)
            elif exps[i][j] == 'N':
                j += 1
                num = 0
                if exps[i][j] == '^':
                    j += 1
                    while isdigit(exps[i][j]):
                        num = num*10 + int(exps[i][j])
                        j += 1
                if num == 0:
                    num = 1
                tmp *= eval('N**%d' % num)
            else:
                j += 1
        if tmp == 1 or tmp == -1:
            l.append((0, ()))
        else:
            l.append((tmp, tuple(sorted(en))))
    
    # construct h
    mp = H(n)
    for val, en in l:
        cols[mp.index(en)] = val
    # print(cols)
    return cols

def EWA(n, elist, NN, alpha):
    mp = H(n)
    var('a')
    S = [X_Complex(n*a)]
    cols = [[1 if i == 0 else 0 for i in range(2^n)]]
    for i in mp[1:]:
        eL, s = R(i, n)
        cols.append(CC(eL, n))
        S.append(X_Complex(s))
    
    alphaA,alphaB = 0, 0
    for i in S:
        alphaA = max(i.a, alphaA)
        alphaB = max(i.b, alphaB)
    # print(alphaA, alphaB)
    D = []
    for i in range(len(S)):
        # print((alphaA-S[i].a), (alphaB - S[i].b))
        D.append(
            int(NN^((alphaA-S[i].a)*alpha + (alphaB - S[i].b)))
        )
    kw = {'N': NN}
    for i in range(len(elist)):
        kw['e%d' % (i+1)] = elist[i]

    B = Matrix(ZZ, Matrix(cols).T(**kw)) * diagonal_matrix(ZZ, D)
    L = B.LLL(0.5)
    v = Matrix(ZZ, L[0])
    x = v * B**(-1)
    phi = int(x[0,1]/x[0,0]*elist[0])
    return phi

def attack(NN, elist, alpha):
    phi = EWA(len(elist), elist, NN, alpha)
    print(phi)
    return phi

e1=5077048237811969427473111225370876122528967447056551899123613461792688002896788394304192917610564149766252232281576990293485239684145310876930997918960070816968829150376875953405420809586267153171717496198336861089523701832098322284501931142889817575816761705044951705530849327928849848158643030693363143757063220584714925893965587967042137557807261154117916358519477964645293471975063362050690306353627492980861008439765365837622657977958069853288056307253167509883258122949882277021665317807253308906355670472172346171177267688064959397186926103987259551586627965406979118193485527520976748490728460167949055289539
e2=12526848298349005390520276923929132463459152574998625757208259297891115133654117648215782945332529081365273860316201130793306570777735076534772168999705895641207535303839455074003057687810381110978320988976011326106919940799160974228311824760046370273505511065619268557697182586259234379239410482784449815732335294395676302226416863709340032987612715151916084291821095462625821023133560415325824885347221391496937213246361736361270846741128557595603052713612528453709948403100711277679641218520429878897565655482086410576379971404789212297697553748292438183065500993375040031733825496692797699362421010271599510269401
e3=12985940757578530810519370332063658344046688856605967474941014436872720360444040464644790980976991393970947023398357422203873284294843401144065013911463670501559888601145108651961098348250824166697665528417668374408814572959722789020110396245076275553505878565603509466220710219260037783849276475397283421068716088638186994778153542817681963059581651103563578804145156157584336712678882995685632615686853980176047683326974283896343322981521150211317597571554542488921290158122634140571148036732893808064119048328855134054709120877895941670166421664806186710346824494054783025733475898081247824887967550418509038276279
NN = 17853303733838066173110417890593704464146824886316456780873352559969742615755294466664439529352718434399552818635352768033531948009737170697566286848710832800426311328560924133698481653594007727877031506265706341560810588064209681809146597572126173303463125668183837840427667101827234752823747483792944536893070188010357644478512143332014786539698535220139784440314481371464053954769822738407808161946943216714729685820896972467020893493349051243983390018762076812868678098172416465691550285372846402991995794349015838868221686216396597327273110165922789814315858462049706255254066724012925815100434953821856854529753
elist = [e1,e2,e3]
c = 1414176060152301842110497098024597189246259172019335414900127452098233943041825926028517437075316294943355323947458928010556912909139739282924255506647305696872907898950473108556417350199783145349691087255926287363286922011841143339530863300198239231490707393383076174791818994158815857391930802936280447588808440607415377391336604533440099793849237857247557582307391329320515996021820000355560514217505643587026994918588311127143566858036653315985177551963836429728515745646807123637193259859856630452155138986610272067480257330592146135108190083578873094133114440050860844192259441093236787002715737932342847147399
alpha = 768 / int(NN).bit_length()				#768指的是d的比特
for i in range(1, len(elist)+1):
    var("e%d" % i)
    var("d%d" % i)
    var("k%d" % i)
g, N, s = var('g'), var('N'), var('s')

for i in range(len(elist)):
    elist[i] = Integer(elist[i])
phi = attack(NN, elist, alpha)

d = gmpy2.invert(65537, phi)
m = int(pow(c, d, NN))
print(libnum.n2s(m))
# hgame{Ext3ndin9_W1en3r's_att@ck_1s_so0o0o_ea3y}

matrix_equation

task.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from Crypto.Util.number import *
import hashlib
from secret import p,q,r
k1=getPrime(256)
k2=getPrime(256)
temp=p*2**256+q*k1+r*k2
hint=len(bin(temp)[2:])
flag='hgame{'+hashlib.sha256(str(p+q+r).encode()).hexdigest()+'}'
print(f'hint={hint}')
print(f'k1={k1}')
print(f'k2={k2}')
"""
83
k1=73715329877215340145951238343247156282165705396074786483256699817651255709671
k2=61361970662269869738270328523897765408443907198313632410068454223717824276837
"""

构造格

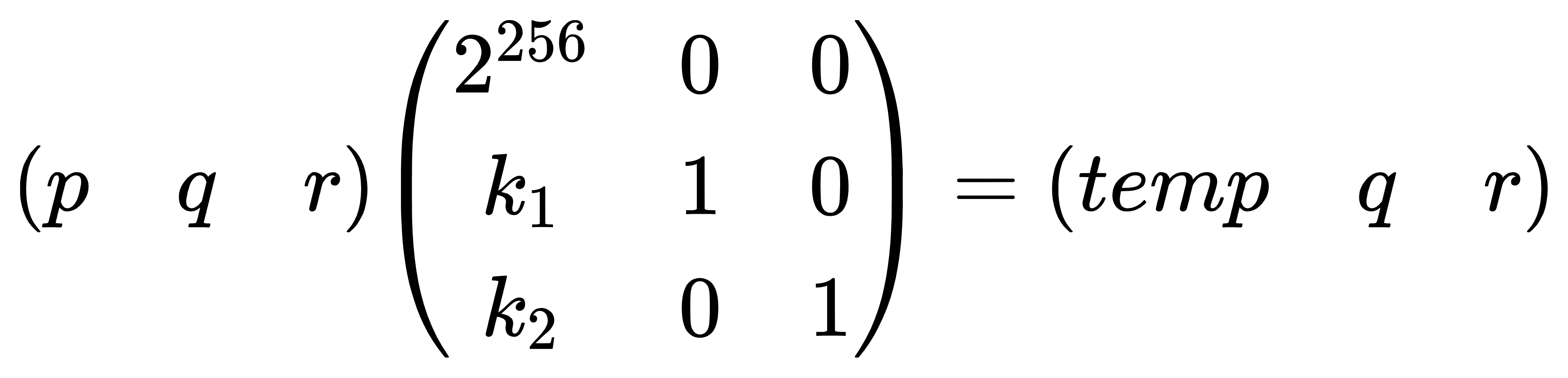
因为$temp \approx 2^{83}$，不需要调整格的大小

HNP

task.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from Crypto.Util.number import *
from secret import flag

def encrypt(m,p,t):
    return [(ti*m)%p for ti in t]

m=bytes_to_long(flag[:63])
length=m.bit_length()+8
p=getStrongPrime(length)
n=32
t=[getRandomRange(0,p) for _ in range(n)]
enc=encrypt(m,p,t)
res=[i%(2**n+1) for i in enc]

print(f'p={p}')
print(f't={t}')
print(f'res={res}')

"""
p=11306299241774950053269547103284637414407835125777245204069367567691021928864773207548731051592853515206232365901169778048084146520829032339328263913558053
t=[3322008555255129336821309701482996933045379792432532251579564581211072677403244970423357912298444457457306659801200188166569132560659008356952740599371688, 8276764260264858811845211578415023343942634613522088631021199433066924291049858607045960690574035761370394263154981351728494309737901121703288822616367266, 9872291736922974456420418463601129094227231979218385985149661132792467621940722580745327835405374826293791332815176458750548942757024017382881517284991646, 4021521745142535813153669961146457406640791935844796005344073886289668464885011415887755787903927824762833158130615018326666118383128627535623639046817799, 24569151076141700493541155834378165089870615699969211988778938492838766214386066952596557490584021813819164202001474086538804476667616708172536787956586, 3218501156520848572861458831123822689702035242514803505049101779996231750875036344564322600086861361414609201214822262908428091097382781770850929067404210, 3563405987398375076327633444036492163004958714828685846202818610320439306396912425420391070117069875583786819323173342951172594046652017297552813501557159, 4914709045693863038598225124534515048993310770286105070725513667435983789847547225180024824321458761262390817487861675595466513538901373422149236133926354, 10800566112999947911006702454427389510409658644419749067440812458744391509925306994806187389406032718319773665587324010542068486131582672363925769248595266, 623364920052209790798128731089194813138909691039137935275037339503622126325928773037501254722851684318024014108149525215083265733712809162344553998427324, 4918421097628430613801265525870561041230011029818851291086862970508621529074497601678774921285912745589840510459677522074887576152015356984592589649844431, 7445733357215847370070696136653689748718028080364812263947785747353258936968978183471549706166364243148972154215055224857918834937707555053246184822095602, 9333534755049225627530284249388438694002602645047933865453159836796667198966058177988500184073454386184080934727537200575457598976121667373801441395932440, 5010854803179970445838791575321127911278311635230076639023411571148488903400610121248617307773872612743228998892986200202713496570375447255258630932158822, 6000645068462569819648461070140557521144801013490106632356836325002546400871463957228581143954591005398533252218429970486115490535584071786260818773166324, 8007260909124669381862034901556111245780505987082990804380814797200322228942432673939944693062470178256867366602331612363176408356304641672459456517978560, 10179739175373883376929532026389135792129233730601278687507041429438945598523995700184622359660605910932803141785598758326254886448481046307666042835829725, 8390072767717395701926289779433055672863880336031837009119103448675232362942223633129328309118158273835961567436591234922783953373319767835877266849545292, 7875011911562967874676113680693929230283866841475641162854665293111344467709424408623198370942797099964625447512797138192853009126888853283526034411007513, 5293772811020012501020124775214770193234655210319343058648675411115210453680753070042821835082619634341500680892323002118953557746116918093661769464642068, 2613797279426774540306461931319193657999892129844832159658771717387120246795689678231275371499556522396061591882431426310841974713419974045883021613987705, 9658126012133217804126630005236073513485215390812977974660029053522665282550965040288256074945246850744694519543358777252929661561636241161575937061521711, 2982535220844977621775139406357528876019349385634811795480230677982345697183586203669094998039995683973939721644887543907494963824968042199353945120367505, 107289984878191849357180490850397539311037762262082755398160292401340078782643246498566039415279868796667596686125847400130898160017838981308638814854641, 120993130590874228473811314869823704699012435303134640953201808807618070048912918046616664677916248813062043597607873728870402493717351447905456920806865, 2253040652771796284266254261719805768102740653097446325869783812201171144150768875885963729324915714812719138247784194752636928267712344736198611708630089, 8650007272154283057350664311505887535841268767424545016901418989555620869091145651216448723200240914143882774616678968725523914310965356875681207295242434, 9628747829107584650014156079928108801687158029086221730883999749044532846489666115473993005442192859171931882795973774131309900021287319059216105939670757, 10846936951522093706092027908131679912432689712451920718439096706435533926996215766191967052667966065917006691565771695772798711202812180782901250249613072, 1606865651227988736664127021678689299989045439998336603562232908863405778474520915170766771811336319655792746590981740617823564813573118410064976081989237, 6239063657591721097735049409610872941214078699330136826592958549212481802973973104374548555184907929255031570525343007518434357690480429981016781110249612, 1855365916387114620581029939707053701062476745235578683558063796604744448050278138954359506922875967537567359575662394297579958372107484276360920567730458]
res=[2150646508, 1512876052, 2420557546, 2504482055, 892924885, 213721693, 2708081441, 1242578136, 717552493, 3210536920, 2868728798, 1873446451, 645647556, 2863150833, 2481560171, 2518043272, 3183116112, 3032464437, 934713925, 470165267, 1104983992, 194502564, 1621769687, 3844589346, 21450588, 2520267465, 2516176644, 3290591307, 3605562914, 140915309, 3690380156, 3646976628]
"""

根据题意有
$$
enc_i \equiv t_i \times m \mod p
$$
且$res_i \equiv enc_i \mod (2^{32} + 1)$

记$enc_i$的高位为$R_{ihigh}$,$res_i$为$r_i$

所以有
$$
R_{ihigh}\times (2^{32} + 1) + r_i \equiv t_i \times m \mod p
$$
把$R_{ihigh}$单独放左边有
$$
R_{ihigh} \equiv (t_i \times m -r_i) \times (2^{32}+1)^{-1} \mod p
$$
即
$$
R_{ihigh} = (t_i\times m - r_i)\times (2^{32}+1)^{-1} +k_i \times p
$$
即inv = $(2^{32} + 1)^{-1}$

构造格

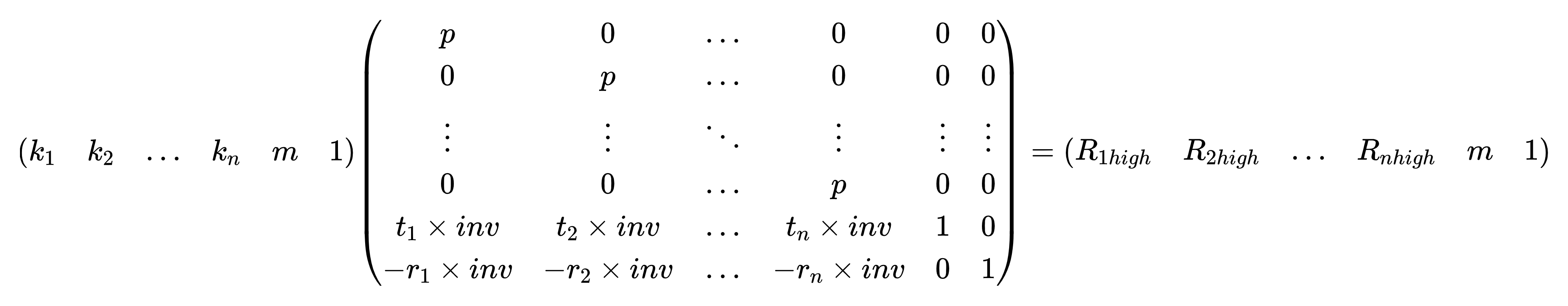
根据$p = 512bit$，推出$m = 504bit$，$R_{ihigh} = 480bit$

调整格为

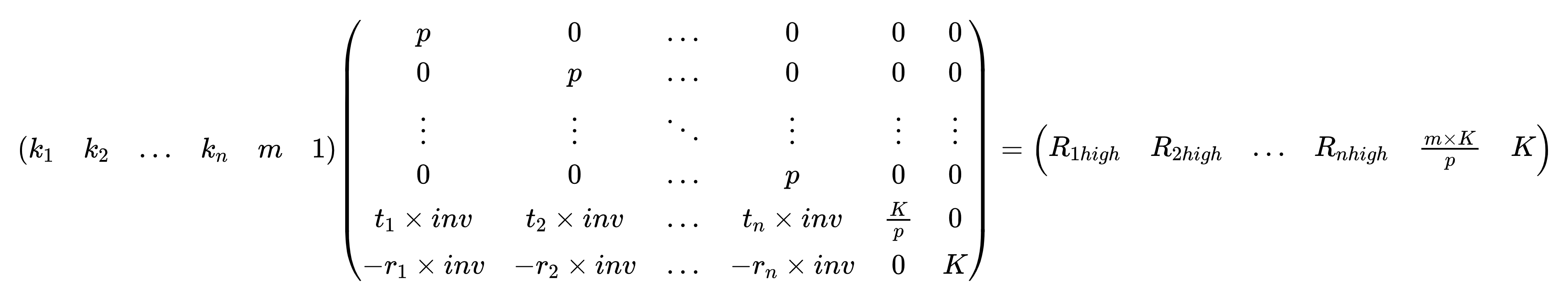
其中$K = 2^{480}$

exp:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
from Crypto.Util.number import *
import gmpy2

p = 11306299241774950053269547103284637414407835125777245204069367567691021928864773207548731051592853515206232365901169778048084146520829032339328263913558053
B = [3322008555255129336821309701482996933045379792432532251579564581211072677403244970423357912298444457457306659801200188166569132560659008356952740599371688, 8276764260264858811845211578415023343942634613522088631021199433066924291049858607045960690574035761370394263154981351728494309737901121703288822616367266, 9872291736922974456420418463601129094227231979218385985149661132792467621940722580745327835405374826293791332815176458750548942757024017382881517284991646, 4021521745142535813153669961146457406640791935844796005344073886289668464885011415887755787903927824762833158130615018326666118383128627535623639046817799, 24569151076141700493541155834378165089870615699969211988778938492838766214386066952596557490584021813819164202001474086538804476667616708172536787956586, 3218501156520848572861458831123822689702035242514803505049101779996231750875036344564322600086861361414609201214822262908428091097382781770850929067404210, 3563405987398375076327633444036492163004958714828685846202818610320439306396912425420391070117069875583786819323173342951172594046652017297552813501557159, 4914709045693863038598225124534515048993310770286105070725513667435983789847547225180024824321458761262390817487861675595466513538901373422149236133926354, 10800566112999947911006702454427389510409658644419749067440812458744391509925306994806187389406032718319773665587324010542068486131582672363925769248595266, 623364920052209790798128731089194813138909691039137935275037339503622126325928773037501254722851684318024014108149525215083265733712809162344553998427324, 4918421097628430613801265525870561041230011029818851291086862970508621529074497601678774921285912745589840510459677522074887576152015356984592589649844431, 7445733357215847370070696136653689748718028080364812263947785747353258936968978183471549706166364243148972154215055224857918834937707555053246184822095602, 9333534755049225627530284249388438694002602645047933865453159836796667198966058177988500184073454386184080934727537200575457598976121667373801441395932440, 5010854803179970445838791575321127911278311635230076639023411571148488903400610121248617307773872612743228998892986200202713496570375447255258630932158822, 6000645068462569819648461070140557521144801013490106632356836325002546400871463957228581143954591005398533252218429970486115490535584071786260818773166324, 8007260909124669381862034901556111245780505987082990804380814797200322228942432673939944693062470178256867366602331612363176408356304641672459456517978560, 10179739175373883376929532026389135792129233730601278687507041429438945598523995700184622359660605910932803141785598758326254886448481046307666042835829725, 8390072767717395701926289779433055672863880336031837009119103448675232362942223633129328309118158273835961567436591234922783953373319767835877266849545292, 7875011911562967874676113680693929230283866841475641162854665293111344467709424408623198370942797099964625447512797138192853009126888853283526034411007513, 5293772811020012501020124775214770193234655210319343058648675411115210453680753070042821835082619634341500680892323002118953557746116918093661769464642068, 2613797279426774540306461931319193657999892129844832159658771717387120246795689678231275371499556522396061591882431426310841974713419974045883021613987705, 9658126012133217804126630005236073513485215390812977974660029053522665282550965040288256074945246850744694519543358777252929661561636241161575937061521711, 2982535220844977621775139406357528876019349385634811795480230677982345697183586203669094998039995683973939721644887543907494963824968042199353945120367505, 107289984878191849357180490850397539311037762262082755398160292401340078782643246498566039415279868796667596686125847400130898160017838981308638814854641, 120993130590874228473811314869823704699012435303134640953201808807618070048912918046616664677916248813062043597607873728870402493717351447905456920806865, 2253040652771796284266254261719805768102740653097446325869783812201171144150768875885963729324915714812719138247784194752636928267712344736198611708630089, 8650007272154283057350664311505887535841268767424545016901418989555620869091145651216448723200240914143882774616678968725523914310965356875681207295242434, 9628747829107584650014156079928108801687158029086221730883999749044532846489666115473993005442192859171931882795973774131309900021287319059216105939670757, 10846936951522093706092027908131679912432689712451920718439096706435533926996215766191967052667966065917006691565771695772798711202812180782901250249613072, 1606865651227988736664127021678689299989045439998336603562232908863405778474520915170766771811336319655792746590981740617823564813573118410064976081989237, 6239063657591721097735049409610872941214078699330136826592958549212481802973973104374548555184907929255031570525343007518434357690480429981016781110249612, 1855365916387114620581029939707053701062476745235578683558063796604744448050278138954359506922875967537567359575662394297579958372107484276360920567730458]
R = [2150646508, 1512876052, 2420557546, 2504482055, 892924885, 213721693, 2708081441, 1242578136, 717552493, 3210536920, 2868728798, 1873446451, 645647556, 2863150833, 2481560171, 2518043272, 3183116112, 3032464437, 934713925, 470165267, 1104983992, 194502564, 1621769687, 3844589346, 21450588, 2520267465, 2516176644, 3290591307, 3605562914, 140915309, 3690380156, 3646976628]
inv = gmpy2.invert(2^32+1,p)

pbits = 512
lbits = 32
kbits = pbits - lbits
n = len(R)

M = Matrix(QQ,n+2,n+2)
for i in range(n):
    M[i,i] = p
    M[-2,i] = B[i]*inv
    M[-1,i] = -R[i]*inv

t = QQ(2^kbits / p)
K = 2^kbits

M[-2,-2] = t
M[-1,-1] = K

for line in M.LLL():
    if abs(line[-1]) == K:
        secret = abs(line[-2]) // t
        print(secret)
flag = long_to_bytes(int(secret))
print(flag)
# hgame{H1dd3n_Numb3r_Pr0bl3m_has_diff3rent_s1tuati0n}

Week4

lastRSA

task.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
from Crypto.Util.number import *
from secret import flag

def encrypt(P,k,leak0):
    round=40
    t=114514
    x= leak0+2*t if k==1 else 2*t*leak0
    enc=2024
    while(round):
        enc+=pow(x,round,P)
        round-=1
    return enc

m=bytes_to_long(flag)
p=getStrongPrime(512)
q=getStrongPrime(512)
assert len(bin(p)[2:])==512 and len(bin(q)[2:])==512
e=0x10001
leak0=p^(q>>13)
n=p*q
enc1=encrypt(n,1,leak0)
enc2=encrypt(n,0,leak0)
c=pow(m,e,n)

print(f"enc1={enc1}")
print(f"enc2={enc2}")
print(f"c={c}")
print(f"n={n}")

"""
enc1=2481998981478152169164378674194911111475668734496914731682204172873045273889232856266140236518231314247189371709204253066552650323964534117750428068488816244218804456399611481184330258906749484831445348350172666468738790766815099309565494384945826796034182837505953580660530809234341340618365003203562639721024   
enc2=2892413486487317168909532087203213279451225676278514499452279887449096190436834627119161155437012153025493797437822039637248773941097619806471091066094500182219982742574131816371999183859939231601667171386686480639682179794271743863617494759526428080527698539121555583797116049103918578087014860597240690299394   
c=87077759878060225287052106938097622158896106278756852778571684429767457761148474369973882278847307769690207029595557915248044823659812747567906459417733553420521047767697402135115530660537769991893832879721828034794560921646691417429690920199537846426396918932533649132260605985848584545112232670451169040592        
n=136159501395608246592433283541763642196295827652290287729738751327141687762873360488671062583851846628664067117347340297084457474032286451582225574885517757497232577841944028986878525656103449482492190400477852995620473233002547925192690737520592206832895895025277841872025718478827192193010765543046480481871       
"""

先求leak，再剪枝。这里剪枝的代码参考DASCTF七月赛

求leak用到了富兰克林相关消息攻击+HGCD

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
from Crypto.Util.number import long_to_bytes
from tqdm import trange
import sys
import gmpy2

def HGCD(a, b):
    if 2 * b.degree() <= a.degree() or a.degree() == 1:
        return 1, 0, 0, 1
    m = a.degree() // 2
    a_top, a_bot = a.quo_rem(x^m)
    b_top, b_bot = b.quo_rem(x^m)
    R00, R01, R10, R11 = HGCD(a_top, b_top)
    c = R00 * a + R01 * b
    d = R10 * a + R11 * b
    q, e = c.quo_rem(d)
    d_top, d_bot = d.quo_rem(x^(m // 2))
    e_top, e_bot = e.quo_rem(x^(m // 2))
    S00, S01, S10, S11 = HGCD(d_top, e_top)
    RET00 = S01 * R00 + (S00 - q * S01) * R10
    RET01 = S01 * R01 + (S00 - q * S01) * R11
    RET10 = S11 * R00 + (S10 - q * S11) * R10
    RET11 = S11 * R01 + (S10 - q * S11) * R11
    return RET00, RET01, RET10, RET11
    
def GCD(a, b):
    print(a.degree(), b.degree())
    q, r = a.quo_rem(b)
    if r == 0:
        return b
    R00, R01, R10, R11 = HGCD(a, b)
    c = R00 * a + R01 * b
    d = R10 * a + R11 * b
    if d == 0:
        return c.monic()
    q, r = c.quo_rem(d)
    if r == 0:
        return d
    return GCD(d, r)

sys.setrecursionlimit(500000)

e = 65537
c = 87077759878060225287052106938097622158896106278756852778571684429767457761148474369973882278847307769690207029595557915248044823659812747567906459417733553420521047767697402135115530660537769991893832879721828034794560921646691417429690920199537846426396918932533649132260605985848584545112232670451169040592        
n = 136159501395608246592433283541763642196295827652290287729738751327141687762873360488671062583851846628664067117347340297084457474032286451582225574885517757497232577841944028986878525656103449482492190400477852995620473233002547925192690737520592206832895895025277841872025718478827192193010765543046480481871       
enc1 = 2481998981478152169164378674194911111475668734496914731682204172873045273889232856266140236518231314247189371709204253066552650323964534117750428068488816244218804456399611481184330258906749484831445348350172666468738790766815099309565494384945826796034182837505953580660530809234341340618365003203562639721024   
enc2 = 2892413486487317168909532087203213279451225676278514499452279887449096190436834627119161155437012153025493797437822039637248773941097619806471091066094500182219982742574131816371999183859939231601667171386686480639682179794271743863617494759526428080527698539121555583797116049103918578087014860597240690299394   
pad1 = 114514*2

R.<x> = PolynomialRing(Zmod(n))
f = 2024 + (x+pad1)^40 + (x+pad1)^39 + (x+pad1)^38 + (x+pad1)^37 + (x+pad1)^36 + (x+pad1)^35 + (x+pad1)^34 + (x+pad1)^33 + (x+pad1)^32 + (x+pad1)^31 + (x+pad1)^30 + (x+pad1)^29 + (x+pad1)^28 + (x+pad1)^27 + (x+pad1)^26 + (x+pad1)^25 + (x+pad1)^24 + (x+pad1)^23 + (x+pad1)^22 + (x+pad1)^21 + (x+pad1)^20 + (x+pad1)^19 + (x+pad1)^18 + (x+pad1)^17 + (x+pad1)^16 + (x+pad1)^15 + (x+pad1)^14 + (x+pad1)^13 + (x+pad1)^12 + (x+pad1)^11 + (x+pad1)^10 + (x+pad1)^9 + (x+pad1)^8 + (x+pad1)^7 + (x+pad1)^6 + (x+pad1)^5 + (x+pad1)^4 + (x+pad1)^3 + (x+pad1)^2 + (x+pad1)^1 - enc1
g = 2024 + (x*pad1)^40 + (x*pad1)^39 + (x*pad1)^38 + (x*pad1)^37 + (x*pad1)^36 + (x*pad1)^35 + (x*pad1)^34 + (x*pad1)^33 + (x*pad1)^32 + (x*pad1)^31 + (x*pad1)^30 + (x*pad1)^29 + (x*pad1)^28 + (x*pad1)^27 + (x*pad1)^26 + (x*pad1)^25 + (x*pad1)^24 + (x*pad1)^23 + (x*pad1)^22 + (x*pad1)^21 + (x*pad1)^20 + (x*pad1)^19 + (x*pad1)^18 + (x*pad1)^17 + (x*pad1)^16 + (x*pad1)^15 + (x*pad1)^14 + (x*pad1)^13 + (x*pad1)^12 + (x*pad1)^11 + (x*pad1)^10 + (x*pad1)^9 + (x*pad1)^8 + (x*pad1)^7 + (x*pad1)^6 + (x*pad1)^5 + (x*pad1)^4 + (x*pad1)^3 + (x*pad1)^2 + (x*pad1)^1 - enc2

res = GCD(f,g)

leak = int(-res.monic().coefficients()[0])
print(f"leak = {leak}")

def findp(p,q):
    if len(p) == 512:
        pp = int(p,2)
        if n % pp == 0:
            p = pp
            q = n // p
            print("p = ",p)
            print("q = ",n // q)
            d = gmpy2.invert(e,(p-1)*(q-1))
            m = pow(c,d,n)
            print(long_to_bytes(int(m)))
            
    else:
        l = len(p)
        pp = int(p,2)
        qq = int(q,2)
        if (pp ^^ (qq >> 13)) % (2 ** l) == leak %(2**l) and pp * qq %(2 ** l) == n % (2**l):
            findp('1' + p,'1' + q)
            findp('1' + p,'0' + q)
            findp('0' + p,'1' + q)
            findp('0' + p,'0' + q)
            
for i in trange(2**14,2**13,-1):
    findp('1',bin(i)[2:])
    # hgame{Gr0bn3r_ba3ic_0ften_w0rk3_w0nd3rs}

看flag的意思应该要用gb基来完成

transformation

task.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#!/usr/bin/env python
# coding: utf-8



from Crypto.Util.number import *
from secret import Curve,gx,gy

# flag = "hgame{" + hex(gx+gy)[2:] + "}"

def ison(C, P):
    c, d, p = C
    u, v = P
    return (u**2 + v**2 - c**2 * (1 + d * u**2*v**2)) % p == 0

def add(C, P, Q):
    c, d, p = C
    u1, v1 = P
    u2, v2 = Q
    assert ison(C, P) and ison(C, Q)
    u3 = (u1 * v2 + v1 * u2) * inverse(c * (1 + d * u1 * u2 * v1 * v2), p) % p
    v3 = (v1 * v2 - u1 * u2) * inverse(c * (1 - d * u1 * u2 * v1 * v2), p) % p
    return (int(u3), int(v3))

def mul(C, P, m):
    assert ison(C, P)
    c, d, p = C
    B = bin(m)[2:]
    l = len(B)
    u, v = P
    PP = (-u, v)
    O = add(C, P, PP)
    Q = O
    if m == 0:
        return O
    elif m == 1:
        return P
    else:
        for _ in range(l-1):
            P = add(C, P, P)
        m = m - 2**(l-1)
        Q, P = P, (u, v)
        return add(C, Q, mul(C, P, m))

c, d, p = Curve

G = (gx, gy)
P = (423323064726997230640834352892499067628999846, 44150133418579337991209313731867512059107422186218072084511769232282794765835)
Q = (1033433758780986378718784935633168786654735170, 2890573833121495534597689071280547153773878148499187840022524010636852499684)
S = (875772166783241503962848015336037891993605823, 51964088188556618695192753554835667051669568193048726314346516461990381874317)
T = (612403241107575741587390996773145537915088133, 64560350111660175566171189050923672010957086249856725096266944042789987443125)
assert ison(Curve, P) and ison(Curve, Q) and ison(Curve, G)
e = 0x10001
print(f"eG = {mul(Curve, G, e)}")

# eG = (40198712137747628410430624618331426343875490261805137714686326678112749070113, 65008030741966083441937593781739493959677657609550411222052299176801418887407)

参考SICTF的那道题

先恢复扭曲爱德华曲线的参数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
import gmpy2

def Get_A(G1,G2):
    x1,y1 = G1
    x2,y2 = G2
    A = x1^2 - x2^2 + y1^2 - y2^2
    return A

def Get_B(G1,G2):
    x1,y1 = G1
    x2,y2 = G2
    B = x1^2*y1^2 - x2^2*y2^2
    return B

def Get_p(G1,G2,G3,G4):
    A12,B12 = Get_A(G1,G2),Get_B(G1,G2)
    A34,B34 = Get_A(G3,G4),Get_B(G3,G4)
    temp1 = A12 * B34 - B12 * A34
    A13,B13 = Get_A(G1,G3),Get_B(G1,G3)
    A24,B24 = Get_A(G2,G4),Get_B(G2,G4)
    temp2 = A13 * B24 - B13 * A24
    may_p = gmpy2.gcd(temp1,temp2)
    
    for i in range(2,2^16):
        if may_p % i == 0:
            may_p = may_p // i
    return may_p

def get_c_d(G1,G2,p):
    A12,B12 = Get_A(G1,G2),Get_B(G1,G2)
    ccd = (A12*gmpy2.invert(B12,p)) % p
    x1,y1 = G1
    cc = (x1^2 + y1^2 - ccd * x1^2 * y1^2) % p
    d = (x1^2 + y1^2 - cc) * gmpy2.invert(cc*x1^2*y1^2,p) % p
    F = Zmod(p)
    c = F(cc).sqrt()
    return c,d

P = (423323064726997230640834352892499067628999846, 44150133418579337991209313731867512059107422186218072084511769232282794765835)
Q = (1033433758780986378718784935633168786654735170, 2890573833121495534597689071280547153773878148499187840022524010636852499684)
S = (875772166783241503962848015336037891993605823, 51964088188556618695192753554835667051669568193048726314346516461990381874317)
T = (612403241107575741587390996773145537915088133, 64560350111660175566171189050923672010957086249856725096266944042789987443125)

p = Get_p(P,Q,S,T)
c,d = get_c_d(P,Q,p)

print(f"p = {p}")
print(f"c = {c}")
print(f"d = {d}")

# p = 67943764351073247630101943221474884302015437788242536572067548198498727238923
# c = 7143899698109428282870539364581968579753042129945786627292343174759297201080
# d = 8779982120820562807260290996171144226614358666469579196351820160975526615300

这题不同之处在于要乘上$e^{-1} \mod order$来恢复在weis的G点，再映射回爱德华曲线

Exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#sage
from Crypto.Util.number import *

p = 67943764351073247630101943221474884302015437788242536572067548198498727238923
# c = 60799864652963819347231403856892915722262395658296749944775205023739430037843
c = 7143899698109428282870539364581968579753042129945786627292343174759297201080
d = 8779982120820562807260290996171144226614358666469579196351820160975526615300
a = 1

P.<z> = PolynomialRing(Zmod(p))
aa = a
dd = (d*c^4)%p
J = (2*(aa+dd)*inverse(aa-dd,p))%p
K = (4*inverse(aa-dd,p))%p
A = ((3-J^2)*inverse(3*K^2,p))%p
B = ((2*J^3-9*J)*inverse(27*K^3,p))%p

for i in  P(z^3+A*z+B).roots():
    alpha = int(i[0])
    for j in P(z^2-(3*alpha^2+A)).roots():
        s = int(j[0])
        s = inverse(s, p)
        if J==alpha*3*s%p:
            Alpha = alpha
            S = s

def twist_to_weier(x,y):
    v = x*inverse(c,p)%p
    w = y*inverse(c,p)%p
    assert (aa*v^2+w^2)%p==(1+dd*v^2*w^2)%p
    s = (1+w)*inverse(1-w,p)%p
    t = s*inverse(v,p)%p
    assert (K*t^2)%p==(s^3+J*s^2+s)%p
    xW = (3*s+J) * inverse(3*K, p) % p
    yW = t * inverse(K, p) % p
    assert yW^2 % p == (xW^3+A*xW+B) % p
    return (xW,yW)
 
def weier_to_twist(x,y):
    xM=S*(x-Alpha)%p
    yM=S*y%p
    assert (K*yM^2)%p==(xM^3+J*xM^2+xM)%p
    xe = xM*inverse(yM,p)%p
    ye = (xM-1)*inverse(xM+1,p)%p
    assert (aa*xe^2+ye^2)%p==(1+dd*xe^2*ye^2)%p
    xq = xe*c%p
    yq = ye*c%p
    assert (a*xq^2+yq^2)%p==c^2*(1+d*xq^2*yq^2)%p
    return (xq,yq)


eG = (40198712137747628410430624618331426343875490261805137714686326678112749070113, 65008030741966083441937593781739493959677657609550411222052299176801418887407)
e = 0x10001

E = EllipticCurve(GF(p), [A, B])
order = E.order()
eG = twist_to_weier(eG[0], eG[1])
eG = E(eG)
t = inverse(e,order)
G = t*eG
print(G)
G = weier_to_twist(49338299923900164306056143014992557349642478113076310967105225637960726019403   ,3746395175077030354020488043970072705075875018302778769259157124252617333772  )
flag = "hgame{" + hex(G[0]+G[1])[2:] + "}"
print(flag)
# hgame{7c91b51150e2339628f10c5be61d49bbf9471ef00c9b94bb0473feac06303bcc}
-------------已经到底啦！-------------