背包密码
记录背包密码学习过程
始发于2023年8月2日,于2024年7月29日第一次更新,2025年8月17日再次更新
背包密码
在学习背包密码之前,我们需要了解什么是背包问题
背包问题
假定一个背包可以承重$S$,现在有$n$个物品,其重量分别为$a_1,a_2\dots a_n$,试问装哪些物品可以恰好使得背包被装满,而且每个物品最多被装一次。转化成数学式子即是
$$
x_1a_1+x_2a_2+\dots+x_na_n=S
$$
其中$x_i \in {0,1}$
显然我们必须枚举所有的 $n$个物品的组合才能解决这个问题,而复杂度也就是$2^n$,这也就是背包加密的妙处所在。
在谈加密过程之前,先了解一下超递增序列
超递增序列
$\begin{Bmatrix}a_1,a_2,\dots,a_n\end{Bmatrix}$是超递增序列,指的是$a_i>a_1+a_2+\dots+a_{i-1}$,即第$i$个数大于前面$i-1$个数之和,也即$a_i>2a_{i-1}$
当明文和超递增序列依次相乘再求和时
$$
x_1a_1+x_2a_2+\dots+x_na_n=S,x_i=
\begin{Bmatrix}
0,1
\end{Bmatrix},
a_i>0
$$
我们可以通过依次比较S与序列中最大的元素大小关系,来确定该元素性质
例如,当$S>a_n$时,说明$x_n=1$
接下来,令$S=S-a_n$,再比较$S$与$r_{n-1}$
通过$n$次比较,我们即可获得所有$x$的值
背包加密算法流程如下:
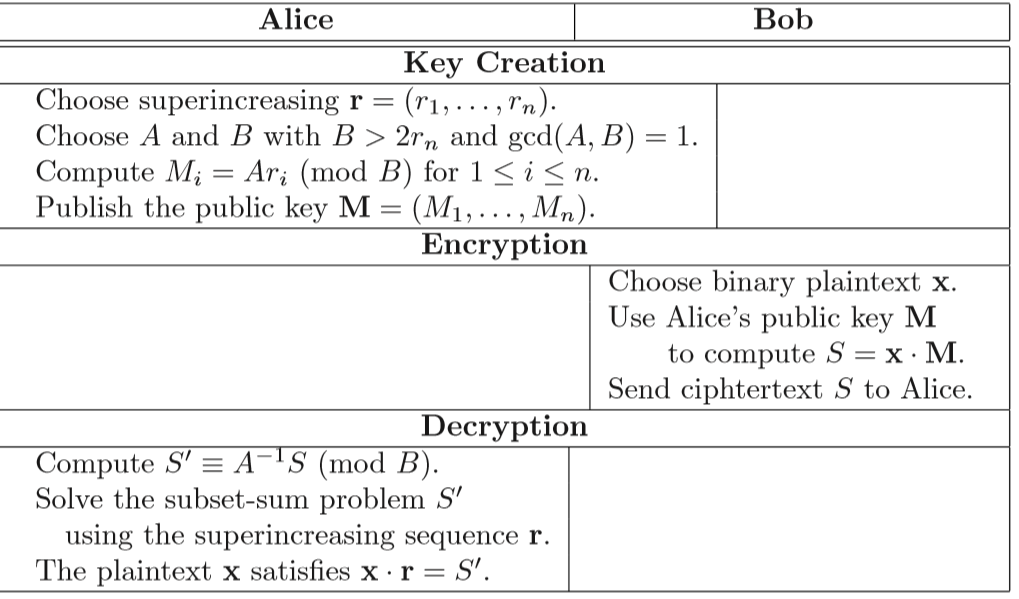
Encryption
- 明文
明文字符串转成二进制,生成明文序列$x = (x_1,x_2,…,x_n),x_i \in (0,1)$
- 私钥
生成一个超递增序列$r = (r_1,r_2,…,r_n)$作为私钥序列
- 公钥
- 生成模数$B$,满足
$$
B>\sum_{i=1}^{n}r_i
$$
即满足$B > 2r_n$,因为$r$是个超递增序列
生成乘数$A$,满足$gcd(A,B)=1$
生成公钥序列$M=\begin{Bmatrix}M_1,M_2,\dots,M_n\end{Bmatrix}$,其中$M_i \equiv Ar_i \mod B$
- 密文
通过以下式子生成密文
$$
S = \sum_{i=1}^{n}x_iM_i
$$
最后公开$M,A,B,S$
Decryption
计算$A$关于模$B$的逆元$A^{-1}$
计算$S’$
$$
S’\equiv A^{-1}S \equiv A^{-1}\sum_{i=1}^nx_iM_i\equiv A^{-1}\sum_{i=1}^nx_iAr_i \equiv \sum_{i=1}^nx_ir_i \mod B
$$
利用超递增序列$r$的性质,求解明文的二进制
最后把二进制转为字符串
Attacks
参数不当
如果乘数$A$,超递增序列$r$的大小选取不当,使得$Ar_i<B$,则$Ar_i \mod B = Ar_i$,这就导致公钥序列$M$是个很明显的超递增序列。
DASCTF5月赛——knapsack
题目:
1 | from Crypto.Util.number import * |
首先注意到key1是个超递减的序列,而且乘数A非常小。
所以$A$和序列中两个最小值相乘的结果很有可能小于$B$,这样我们可以通过序列中两个最小值求$gcd$来获得$A$,
我们先假设最小的是$a_0$,$a_0,a_1,…,a_n$依次增大
如果能找到两个数满足$a_{i+1}<a_i$,这就说明从$a_i$到$a_{i+1}$存在一次模运算
$$
A \times a_{i+1}=A \times 2a_i \mod B
$$
所以有
$$
B = A(2a_i-a_{i+1})
$$
参考:DASCTF五月月赛 暨 BJDCTF 3rd 部分WP-安全客 - 安全资讯平台 (anquanke.com)
背包密码求解
实际遇到的CTF题,基本都不会按上面那个加解密流程出题,经常遇到的都是形如
$$
S = \sum_{i=0}^{n-1}x_iM_i
$$
其中$M$为背包的公钥,$S$为密文,记$n = \mathrm{len}(M)$,背包密度$d = \frac{n}{\log_2(\max(M))}$。
当密度$d <0.9408$时,可以用LLL、BKZ算法来完成求解(但这里我感觉过于草率,做了各个比赛的背包题之后有个疑问:密度在什么范围用LLL,在什么范围用BKZ,block_size又该怎么选取)。
求解过程其实就用公钥序列$M= (M_1,M_2,…,M_n)$构造两种格
Lattice1
第一种是$(n+1)\times (n+1)$的格:
$$
\begin{pmatrix}
1 & 0 & … & 0 & M_1\\
0 & 1 & … & 0 & M_2\\
\vdots & \vdots & \ddots & \vdots & \vdots \\
0 & 0 & … & 1 &M_n\\
0 & 0 & … & 0 & S
\end{pmatrix}
$$
其线性关系是
$$
\begin{pmatrix}
x_1 & x_2 & … & x_n & -1
\end{pmatrix}
\begin{pmatrix}
1 & 0 & … & 0 & M_1\\
0 & 1 & … & 0 & M_2\\
\vdots & \vdots & \ddots & \vdots & \vdots \\
0 & 0 & … & 1 &M_n\\
0 & 0 & … & 0 & S
\end{pmatrix}
=
\begin{pmatrix}
x_1 & x_2 & … & x_n & 0
\end{pmatrix}
$$
Lattice2
第二种也是$(n+1)\times(n+1)$的格,只不过把对角线元素替换为2,并在最后一行添加1:
$$
\begin{pmatrix}
2 & 0 & … & 0 & M_1\\
0 & 2 & … & 0 & M_2\\
\vdots & \vdots & \ddots & \vdots & \vdots \\
0 & 0 & … & 2 & M_n\\
1 & 1 & … & 1 & S
\end{pmatrix}
$$
这个对应的线性组合是
$$
\begin{pmatrix}
x_1 & x_2 & … & x_n & -1
\end{pmatrix}
\begin{pmatrix}
2 & 0 & … & 0 & M_1\\
0 & 2 & … & 0 & M_2\\
\vdots & \vdots & \ddots & \vdots & \vdots \\
0 & 0 & … & 2 &M_n\\
1 & 1 & … & 1 & S
\end{pmatrix}
=
\begin{pmatrix}
2x_1-1 & 2x_2-1 & … & 2x_n-1 & 0
\end{pmatrix}
$$
第二种比第一种好在第二种格的行列式会更大一些
上面两个格一般在用的时候会在最后一列乘上N = ceil(sqrt(n))
带模的背包加密
实际上经常出现带模的背包,形如
$$
S = \sum_{i=0}^{n}x_iM_i \mod p \longrightarrow S = \sum_{i=0}^nx_iM_i - kp
$$
相应格变为
$$
\begin{pmatrix}
x_1 & x_2 & … & x_n & -1 & k
\end{pmatrix}
\begin{pmatrix}
2 & 0 & … & 0 & 0 &M_1\\
0 & 2 & … & 0 & 0 &M_2\\
\vdots & \vdots & \ddots &\vdots& \vdots & \vdots \\
0 & 0 & … & 2 & 0 &M_n\\
0 & 0 & … & 0 & 1 & S\\
1 & 1 & … & 1 & 0 & p
\end{pmatrix}
=
\begin{pmatrix}
2x_1-1 & 2x_2-1 & … & 2x_n-1 &1 & 0
\end{pmatrix}
$$
在做了不少这种题之后,总结出一个点:由于加密消息的长度并不会很长,所以$k$的范围是在可爆破范围内的,我们就可以爆破k,把带模背包转换为不带模的背包进行求解。具体的一个例子是2025LitCTF——newbag
乘法背包
在24年的WKCTF——meet me in the summer赛题中接触到这个概念,并且在赛后学习了处理方法。并在2025年8月17日更新了一下做法
task.py
1 | from random import choice, randint |
我们仅讨论与乘法背包相关的部分。完整的wp可以看 我的另一篇文章
根据题意有
$$
ra \equiv \prod_{i = 0}^{69} a_ik_{i} \mod p
$$
$k_i$表示secret从低往高的第$i$位,需要注意的是当$k_i = 0$的时候是不需要乘进来的,这里只是写成这样。
因为$p-1$光滑,我们考虑把这个式子变成一个求解离散对数的问题,这样才能利用上$p-1$光滑
我们随便取一个生成元$g$,然后对等式两边取对数,要注意的是,取对数之后模数应该变成p-1
$$
\log_{g}{(ra)} \equiv \sum_{i=0}^{69} \log_{g}(a_ik_i) \mod p - 1
$$
对于这个式子,当$k_i = 1$的时候,$log_g^{a_ik_i} = log_g^{a_i}$,刚刚前面说了$k_i =0$的时候是不需要乘进来的,那这个取离散对数后的式子里面只包括了$k_i = 1$的情况。
因此我们有
$$
\log_{g}{(ra)} \equiv \sum_{i=0}^{69} k_i\cdot \log_{g}{(a_i)} \mod p - 1
$$
这样就可以写为加法背包了,这个新的背包密度只有0.13302518379683503,几乎不会有什么卡顿
造下面这个带模的格(在更新这篇文章的时候,我试着爆破$k$转化为不带模的进行求解)
$$
\begin{pmatrix}
k_{70} & k_{69} & … & k_{1} & l & -1
\end{pmatrix}
\begin{pmatrix}
2 & 0 & … & 0 & 0 & \log_{g}{a_0}\\
0 & 2 & … & 0 & 0 & \log_{g}{a_1}\\
\vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\
0 & 0 & … & 2 & 0 & \log_{g}{a_{69}}\\
0 & 0 & … & 0 & 1 & p - 1\\
1 & 1 & … & 1 & 1 & \log_{g}{ra}
\end{pmatrix}
=
\begin{pmatrix}
k_{70}-1 & k_{69}-1 & … & k_1-1 & l-1 & 0
\end{pmatrix}
$$
exp.sage
1 | from tqdm import * |
如何根据不同背包密度选取合适的规约算法以及参数
我利用Lattice1和Lattice2,针对$d \ge 0.4$的每个密度,都取了500组数据并进行5次测试,成功率取得是平均值(block_size=26的时候,密度大于0.8的数据只取10组,因为一轮下来,得8小时,只好把数据量减少一点)
测试代码以及测试结果见:
一些做过的赛题
都2025年了,已经很少有那种造个格直接秒了的背包,接下来我会分享一些我遇到过的题目
MoeCTF2022——MiniMiniBackPack
task.py
1 | from gmpy2 import * |
gen_key生成超递增序列。
$$
c = \sum_{i=0}^{L}key_i^{m_i}
$$
其中$m_i$指的是$m$的第$i$个bit
把$c$依次和序列中最大的值比较即可求解
exp.py
1 | from Crypto.Util.number import * |
MoeCTF2022——knapsack
task.py
1 | from random import randint |
$$
cipher = \sum_{i=0}^{n}msg_i\cdot key_i
$$
$msg_i$是每个字符的ASCII值
可以发现公钥中最大的值大约是1400bit,而背包的长度是44,可见背包密度$d = \frac{n}{\log_2 {(\max(pk)})}$会很小
造这个格即可
$$
\begin{pmatrix}
x_1 & x_2 & … & x_n & -1
\end{pmatrix}
\begin{pmatrix}
1 & 0 & … & 0 & M_1\\
0 & 1 & … & 0 & M_2\\
\vdots & \vdots & \ddots & \vdots & \vdots \\
0 & 0 & … & 1 &M_n\\
0 & 0 & … & 0 & S
\end{pmatrix}
=
\begin{pmatrix}
x_1 & x_2 & … & x_n & 0
\end{pmatrix}
$$
exp.sage
1 | pk = [...] |
2023天融信杯——easybag
1 | import os |
从encrypt(m),我们可以知道$c \equiv key_i×m_i \mod p \longrightarrow c = key_i×m_i+kp$
$$
\therefore 0 = \sum_{i=1}^{80}key_im_i + kp - c
$$
造格
$$
\begin{pmatrix}
1 & 0 & … & 0 & 0 &key_1\\
0 & 1 & … & 0 & 0 & key_2\\
\vdots & \vdots & \ddots & \vdots & \vdots &\vdots \\
0 & 0 & … & 1 &0 & key_n\\
0 & 0 & … & 0 & 1 & c \\
0 & 0 & … & 0 & 0 & p
\end{pmatrix}
$$
exp
1 | from Crypto.Util.number import * |
sagemath中的BKZ()可以设置参数,例如BKZ(block_size = 16),指定了BKZ算法中的块大小。默认情况下是block_size = 20
block_size越大,执行速度越慢,但结果更精确
2025Hgame——ezBag
task.py
1 | from Crypto.Util.number import * |